DT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
29 tháng 10 2018
a) Ta có: A = ax + bx + cx + ay + by + cy + az + bz + cz
= x.(a+b+c) + y.(a+b+c) + z.(a+b+c)
= (a+b+c).(x+y+z) (1)
Lại có: a + b + c = -3 (2)
x + y + z = -6 (3)
Từ (1) ; (2) ; (3) => A = -3.(-6) = 18
Vậy A = 18
b) B = ax - bx - cx - ay + by + cy - az + bz +cz
= x.(a-b-c) - y.(a-b-c) - z.(a-b-c)
= (a-b-c).(x-y-z)
Lại có: a - b - c = 0 ; x - y - z = 2016
=> B = 0.2016 = 0
Vậy B = 0
10 tháng 7 2017
x=by+cz;y=ax+cz;z=ax+by
=>x+y+z=2(ax+by+cz)
\(\Leftrightarrow\frac{x+y+z}{2}=ax+by+cz\)
\(\Leftrightarrow y+z=\frac{x+y+z}{2}+ax;z+x=\frac{x+y+z}{2}+by;x+y=\frac{x+y+z}{2}+cz\)
\(\Leftrightarrow\frac{y+z-x}{2}=ax;\frac{z+x-y}{2}=by;\frac{x+y-z}{2}=cz\)
\(\Leftrightarrow\frac{y+z-x}{2x}=a;\frac{z+x-y}{2y}=b;\frac{x+y-z}{2z}=c\)
\(\Rightarrow A=\frac{1}{1+\frac{x+y-z}{2z}}+\frac{1}{1+\frac{y+z-x}{2x}}+\frac{1}{1+\frac{z+x-y}{2y}}=\frac{1}{\frac{x+y+z}{2x}}+\frac{1}{\frac{x+y+z}{2y}}+\frac{1}{\frac{x+y+z}{2z}}\)
\(=\frac{2x}{x+y+z}+\frac{2y}{x+y+z}+\frac{2z}{x+y+z}=\frac{2\left(x+y+z\right)}{x+y+z}=2\)
SC
2
VT
1 tháng 8 2016
M = ax + ay + bx + by
= a(x + y) + b( x + y)
= (a + b)(x + y)
mà a + b = -5 ; x + y = 13
=> M = (-5).13 = -65
28 tháng 6 2016
a) \(M=ax+bx+ay+by=x\cdot\left(a+b\right)+y\cdot\left(a+b\right)=\left(a+b\right)\cdot\left(x+y\right)=2\cdot17=34.\)
b) \(N=ax-by+bx-ay=a\left(x-y\right)+b\left(x-y\right)=\left(a+b\right)\left(x-y\right)=7\cdot1=7\)
23 tháng 2 2018
a) suy ra a.(x+y)+b.(x+y)
suy ra (x+y) (a+b)
suy ra 17. (-2) = 34
b) suy ra a.(x-y) + b.(x-y)
suy ra (a+b) (x-y)
suy ra (-7).(-1)
mk làm bậy ko bít đúng hay ko
28 tháng 4 2020
a) ax + ay - bx - by
= ax - bx + ay - by
= x( a - b) + y( a -b )
= ( a - b) ( x+y)
= -20 . 5
= -100
b) ax + ay + bx + by
= ax + bx + ay + by
= x( a+ b) + y( a+b)
= ( a+ b) ( x + y)
= - 7 . 17
= -119
hok tốt!!
K
3
12 tháng 6 2017
A= ax - ay + bx - by
= a.(x-y)+b.(x-y)
=(x-y).(a+b)
=5.(-17)-85
12 tháng 6 2017
A = ax - ay + bx - by
A = a . ( x - y ) + b . ( x - y )
A = ( a + b ) . ( x - y )
Vì a + b = -17 và x - y = 5
Thay vào biểu thức, ta được :
A = ( -17 ) . 5
A = -85
Vậy giá trị biểu thức của A là -85
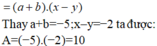
ax + by = 5c (1); by + cz = 5a (2); cz + ax = 5b (3);
Lấy (1) - (2) + (3) về theo vế có : 2ax = - 5a + 5b + 5c => 2a(x + 5) = 5(a + b + c)
=> 1/(x + 5) = 2a/5(a + b + c) (4)
Tương tự :
1/(y + 5) = 2b/5(a + b + c) (5)
1/(z + 5) = 2c/5(a + b + c) (6)
Từ (4) + (5) + (6) :
M = 1/(x + 5) + 1/(y + 5) + 1/(z + 5) = 2/5