Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(x^4-2x^3+\left(m-14\right)x^2+\left(2m+6\right)x-3m+9=0\)
\(\Leftrightarrow x^4-2x^3-14x^2+6x+9+m\left(x^2+2x-3\right)=0\)
\(\Leftrightarrow\left(x^2+2x-3\right)\left(x^2-4x-3\right)+m\left(x^2+2x-3\right)=0\)
\(\Leftrightarrow\left(x^2+2x-3\right)\left(x^2-4x+m-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x^2+2x-3=0\\x^2-4x+m-3=0\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-3\\x^2-4x+m-3=0\left(1\right)\end{matrix}\right.\)
a/ Tập X có đúng 4 phần tử khi và chỉ khi (1) có 2 nghiệm pb khác 1 và -3
\(\Leftrightarrow\left\{{}\begin{matrix}\Delta'=4-\left(m-3\right)>0\\1^2-4.1+m-3\ne0\\\left(-3\right)^2-4.\left(-3\right)+m-3\ne0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m< 7\\m\ne6\\m\ne-18\end{matrix}\right.\)
b/ Do (1) không thể đồng thời có 2 nghiệm \(\left\{{}\begin{matrix}x=1\\x=-3\end{matrix}\right.\) nên X có 2 phần tử khi:
TH1: \(\left(1\right)\) vô nghiệm \(\Leftrightarrow\Delta'< 0\Leftrightarrow m>7\)
TH2: (1) có nghiệm kép \(x=1\) hoặc \(x=-3\)
\(\Rightarrow\left\{{}\begin{matrix}\Delta'=0\\\left[{}\begin{matrix}-\frac{b}{2a}=1\\-\frac{b}{2a}=-3\end{matrix}\right.\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}m=7\\\left[{}\begin{matrix}2=1\\2=-3\end{matrix}\right.\end{matrix}\right.\) (ko có m thỏa mãn)
Vậy \(m>7\)

\(x^3-3mx^2+3mx-1=0\)
\(\Leftrightarrow\left(x-1\right)\left(x^2+x+1\right)-3mx\left(x-1\right)=0\)
=>\(\left(x-1\right)\left(x^2+x-3mx+1\right)=0\)
Để A có 3 phần tử thì \(x^2+x\left(1-3m\right)+1=0\) có hai nghiệm phân biệt
=>\(\left(1-3m\right)^2-4>0\)
=>(3m-1-2)(3m-1+2)>0
=>(3m-3)(3m+1)>0
=>m>1 hoặc m<-1/3


\(\left(x-1\right)\left(x+2\right)\left(x^3+4x\right)=0\\ \Leftrightarrow\left(x-1\right)\left(x+2\right)x\left(x^2+4\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x=1\\x=-2\\x^2=-4\left(vô.lí\right)\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=1\\x=-2\end{matrix}\right.\)
Vậy A có 3 phần tử (B)

Lời giải:
$2x^2-5x+2=0$
$\Leftrightarrow (x-2)(2x-1)=0$
$\Leftrightarrow x=2$ hoặc $x=\frac{1}{2}$
Vậy $A=\left\{2;\frac{1}{2}\right\}$

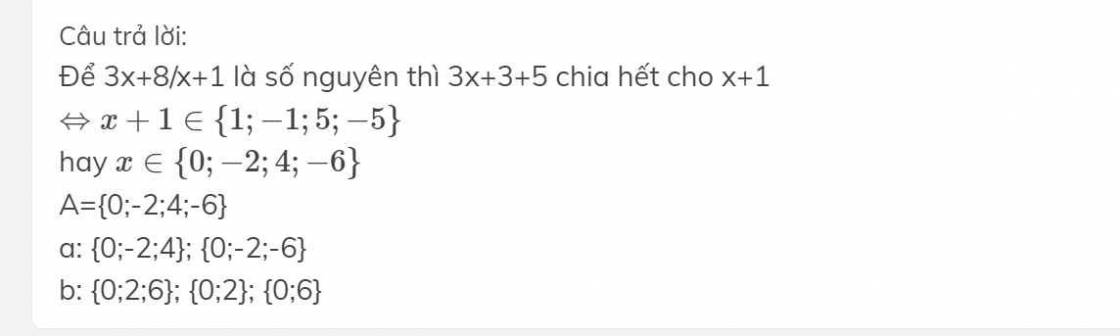
Để 3x+8/x+1 là số nguyên thì 3x+3+5 chia hết cho x+1
\(\Leftrightarrow x+1\in\left\{1;-1;5;-5\right\}\)
hay \(x\in\left\{0;-2;4;-6\right\}\)
A={0;-2;4;-6}
a: {0;-2;4}; {0;-2;-6}
b: {0;2;6}; {0;2}; {0;6}

\(x^2+2\left(m-3\right)x-4m+8=0\) (1)
\(\Leftrightarrow x^2-6x+8+2m\left(x-2\right)=0\)
\(\Leftrightarrow\left(x-2\right)\left(x-4\right)+2m\left(x-2\right)=0\)
\(\Leftrightarrow\left(x-2\right)\left(x-4+2m\right)=0\Rightarrow\left[{}\begin{matrix}x=2\\x=-2m+4\end{matrix}\right.\)
Vậy \(Y=\left\{2;-2m+4\right\}\)
Xét pt \(x^2+4x-2m+10=0\left(2\right)\)
a/ Để \(X\cup Y\)có đúng 4 phần tử \(\Leftrightarrow\) (1) và (2) đều có 2 nghiệm pb và ko có nghiệm chung
\(\Leftrightarrow\left\{{}\begin{matrix}-2m+4\ne2\\\Delta'_{\left(2\right)}=4-\left(-2m+10\right)>0\\2^2+4.2-2m+10\ne0\\\left(-2m+4\right)^2+4.\left(-2m+4\right)-2m+10\ne0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m\ne1\\m>3\\m\ne11\\\left\{{}\begin{matrix}m\ne\frac{7}{2}\\m\ne3\end{matrix}\right.\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}m>3\\m\ne\left\{\frac{7}{2};11\right\}\end{matrix}\right.\)
b/
Để (1) và (2) có (thể có) 2 nghiệm chung
\(\Rightarrow\left\{{}\begin{matrix}2m-6=4\\-4m+8=-2m+10\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}m=5\\m=-1\end{matrix}\right.\) (ko tồn tại m thỏa mãn)
Vậy (1) và (2) luôn có tối đa 1 nghiệm chung
Để (2) có nghiệm \(\Rightarrow\Delta'_{\left(2\right)}\ge0\Rightarrow m\ge3\)
\(X\cap Y\) có 1 phần tử khi và chỉ khi (1) và (2) có 1 nghiệm chung \(\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-2m+4\end{matrix}\right.\) là nghiệm của (2)
TH1: \(x=2\) là nghiệm của (2)
\(\Rightarrow2^2+4.2-2m+10=0\)
\(\Leftrightarrow m=11\)
TH2: \(x=-2m+4\) là nghiệm của (2)
\(\Leftrightarrow\left(-2m+4\right)^2+4\left(-2m+4\right)-2m+10=0\)
\(\Leftrightarrow4m^2-26m+42=0\Leftrightarrow\left[{}\begin{matrix}m=3\\m=\frac{7}{2}\end{matrix}\right.\)
Vậy \(\left[{}\begin{matrix}m=11\\m=3\\m=\frac{7}{2}\end{matrix}\right.\)

\(2x< 3\Rightarrow x< \frac{3}{2}\)
\(\Rightarrow A=\left(-\infty;\frac{3}{2}\right)\)
\(-3x< \sqrt{6}\Rightarrow x>-\frac{\sqrt{6}}{3}\)
\(\Rightarrow B=\left(-\frac{\sqrt{6}}{3};+\infty\right)\)
\(A\cup B=R\)
\(A\backslash B=(-\infty;-\frac{\sqrt{6}}{3}]\)
\(C_R^{A\cup B}=\varnothing\)
\(C_R^{A\backslash B}=B\)
\(A\cap B=\left(-\frac{\sqrt{6}}{3};\frac{3}{2}\right)\) có 2 số nguyên (0 và 1)