
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


b: Ta có: \(x^3-9x^2+27x-27\)
\(=\left(x-3\right)^3\)
\(=\left(-7\right)^3=-343\)
c: Ta có: \(\dfrac{x^3-1}{x^2+1}\)
\(=\dfrac{6^3-1}{6^2+1}=\dfrac{215}{37}\)

a) Thay x=1:
\(9.1^2+12.1+49=70\)
b) Thay x=-2 và y=3:
\(25.\left(-2\right)^2-10\left(-2\right).3+3^2\)\(=169\)
c)Thay x=-10:
\(\left(-10\right)^3+15\left(-10\right)^2+75\left(-10\right)+125=-125\)
d) Thay x=13:
\(13^3-9.13^2+27.13-27=1000\)
e) Thay x=-2:
\(\left(-2-1\right)^3-4\left(-2\right)\left(-2+1\right)\left(-2-1\right)+3\left(-2-1\right)\left[\left(-2\right)^2-2+1\right]\)=-30
f) Thay x=1:
\(\left(1-1\right)\left(1-2\right)\left(1+1+1\right)\left(4+2+1\right)=0\)
\(9x^2+12x+49=\left(9x^2+12x+4\right)+45=\left(3x+2\right)^2+45=5^2+45=25+45=70\)
\(25x^2-10xy+y^2=\left(5x-y\right)^2=\left(-13\right)^2=169\)
\(x^3+15x^2+75x+125=\left(x^3+5x^2\right)+\left(10x^2+50x\right)+\left(25x+125\right)=x^2\left(x+5\right)+10x\left(x+5\right)+25\left(x+5\right)=\left(x+5\right)^2\left(x+5\right)=\left(x+5\right)^3=-125\)
\(x^3-9x^2+27x-27=\left(x^3-3x^2\right)-\left(6x^3-18x\right)+\left(9x-27\right)=x^2\left(x-3\right)-6x\left(x-3\right)+9\left(x-3\right)=\left(x-3\right)^3=1000\)
\(x=1\Rightarrow x-1=0\Rightarrow\left(x-1\right)\left(x-2\right)\left(1+x+x^2\right)\left(4+2x+x^2\right)=0\)

a) \(A=3\left(x+5\right)+x^2\)
Thay x = 1 vào A, ta được:
\(A=3\left(1+5\right)+1^2\)
\(A=3.6+1\)
\(A=19\)
b) \(B=3x\left(x+2\right)-x\left(x+1\right)\)
Thay x = -1 vào B, ta được:
\(B=3.\left(-1\right)\left(-1+2\right)-\left(-1\right)\left(-1+1\right)\)
\(B=-3-0\)
\(B=-3\)
c) \(C=7x\left(x-5\right)+3\left(x-2\right)\)
Thay x = 0 vào C, ta được:
\(C=7.0.\left(0-5\right)+3.\left(0-2\right)\)
\(C=0+3.\left(-2\right)\)
\(C=-6\)
d) \(D=-2x\left(x+1\right)+4\left(x+2\right)\)
Thay x = -1 vào D, ta được:
\(D=-2\left(-1\right)\left(-1+1\right)+4\left(-1+2\right)\)
\(D=0+4\)
\(D=4\)
e) \(E=x^2-x+2x\left(x+3\right)\)
Thay x = 2 vào E, ta được:
\(E=2^2-2+2.2\left(2+3\right)\)
\(E=4-2+4.5\)
\(E=22\)
f) \(F=5-4x\left(x-2\right)\)
Thay x = -1 vào F, ta được:
\(F=5-4.\left(-1\right)\left(-1-2\right)\)
\(F=5-12\)
\(F=-7\)
g) \(G=x\left(x-5\right)-2x\left(x+1\right)+x^2\)
Thay x = -2 vào G, ta được:
\(G=-2\left(-2-5\right)-2.\left(-2\right)\left(-2+1\right)+\left(-2\right)^2\)
\(G=14-4+4\)
\(G=14\)
h) \(H=x\left(7x+2\right)-5x\left(x+3\right)\)
Thay x = 1 vào H, ta được:
\(H=1\left(7.1+2\right)-5.1\left(1+3\right)\)
\(H=9-20\)
\(H=-11\)
i) \(I=3x^2-2x\left(x-5\right)+x\left(x-7\right)\)
Thay x = 10 vào I, ta được:
\(I=3.10^2-2.10\left(10-5\right)+10.\left(10-7\right)\)
\(I=300-100+30\)
\(I=230\)

a, bạn xem lại đề
b, \(\frac{x^3-1}{x^2-1}=\frac{\left(x-1\right)\left(x^2+x+1\right)}{\left(x-1\right)\left(x+1\right)}=\frac{x^2+x+1}{x+1}\)
Thay x = 6 ta được : \(=\frac{36+6+1}{6+1}=\frac{43}{7}\)
c, \(\frac{x^2-2x+1}{x^3-1}+\frac{x^2-1}{\left(x-1\right)^2}=\frac{x-1}{x^2+x+1}+\frac{x+1}{x-1}\)
\(=\frac{x^2-1+x^3+x^2+x+x^2+x+1}{x^3-1}=\frac{x^3+3x^2+2x}{x^3-1}=\frac{x\left(x^2+3x+2\right)}{x^3-1}\)
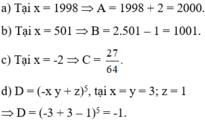
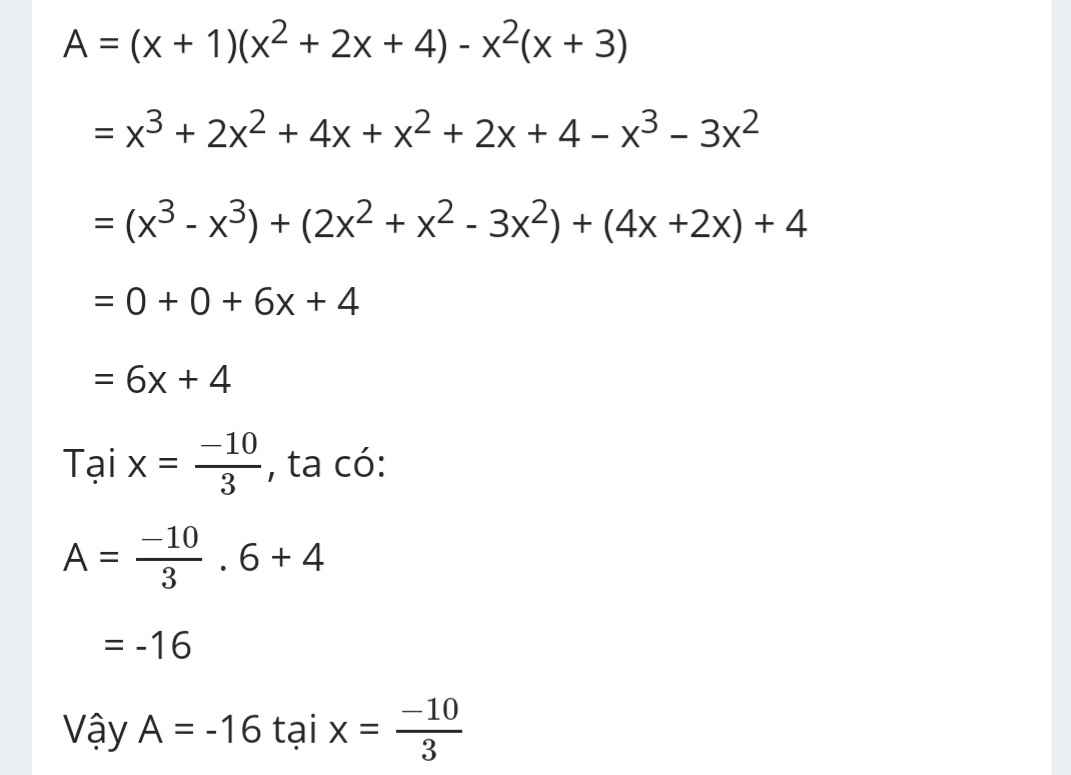
\(A=x^2-9-x^2-x+2=-x-7=-\dfrac{1}{3}-7=-\dfrac{22}{3}\)
\(A=\left(x-3\right)\left(x+3\right)-\left(x+2\right)\left(x-1\right)=x^2-9-\left(x^2+x-2\right)=x^2-9-x^2-x+2=-x-7=-\dfrac{1}{3}-7=-\dfrac{22}{3}\)