Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

ta thấy:
(3x+8 )=(3x+3)+5
=>(3x+3)+5 \(⋮\)(x+1)
=>5\(⋮\)(x+1)
=>(x+1) thuộc Ư(5)={+-1;+-5}
=>
x+1 1 -1 5 -5
x 0 -2 4 -6
vậy x=0:-2:4:-6

Giả sử a<b ( với a,b∈N*)
Ta có tổng của chúng bằng 45.
Vì ƯCLN(a,b)=9 nên:
a=9.m ; b=9.n ( với ƯCLN( m,n)=1 và m<n)
Ta có: 9m+9n = 45
⇒ 9. ( m+n)= 45
⇒ m+n = 45:9
⇒ m+n = 5
Vì ƯCLN(m,n)=1 và m<n nên ta có bảng sau:
| m | 1 | 2 |
| n | 4 | 3 |
⇒
| a | 9 | 18 |
| b | 36 | 27 |
Vậy hai số cần tìm ( a,b)∈{( 9,36); (18,27)}

a) Ta có :
108 = 22 . 33
180 = 22 . 32 . 5
=> ƯCLN( 108 , 180 ) = 22 . 32 = 36
=> ƯC( 108 , 180 ) = Ư( 36 ) = { 1 ; 2 ; 3 ; 4 ; 6 ; 9 ; 12 ; 18 ; 36 }
Mà bài bảo tìm Ư( 108 , 180 ) lớn hơn 15
=> Ta có tập hợp { 18 ; 36 }
b) Ta có :
126 ⋮ x ; 210 ⋮ x ( 15 < x < 20 )
=> x ∈ ƯC( 126 ; 210 )
Ta có :
126 = 2 . 32 . 7
210 = 2 . 3 . 5 . 7
=> ƯCLN( 126 , 210 ) = 2 . 3 . 7 = 42
=> ƯC( 126 , 210 ) = Ư( 42 ) = { 1 ; 2 ; 3 ; 6 ; 7 ; 14 ; 21 ; 42 }
=> x ∈ { 1 ; 2 ; 3 ; 6 ; 7 ; 14 ; 21 ; 42 }
Mà 15 < x < 20
=> x ∈ ∅

- Để tìm hai số tự nhiên a và b thoả mãn a + b = 810 và ước chung lớn nhất của chúng bằng 45, ta có thể sử dụng phương pháp giải hệ phương trình. Gọi UCLN(a, b) là ước chung lớn nhất của a và b.
Vì UCLN(a, b) = 45, ta có thể viết a = 45x và b = 45y, với x và y là các số tự nhiên. Thay vào phương trình a + b = 810, ta có 45x + 45y = 810, hay x + y = 18.
Bây giờ ta cần tìm hai số tự nhiên x và y thoả mãn x + y = 18. Có nhiều cách để làm điều này, ví dụ như x = 9 và y = 9. Khi đó, a = 45x = 45 * 9 = 405 và b = 45y = 45 * 9 = 405.
Vậy, hai số tự nhiên a và b là 405 và 405.
- Để tìm hai số nguyên tố p và q thoả mãn p > q và p + q cũng như p - q đều là số nguyên tố, ta cần kiểm tra các số nguyên tố và tìm hai số thoả mãn yêu cầu.
Có nhiều cách để làm điều này, ví dụ như kiểm tra từng số nguyên tố theo thứ tự tăng dần và kiểm tra điều kiện p + q và p - q cũng là số nguyên tố.
Ví dụ:
- Kiểm tra số nguyên tố đầu tiên là 2. Ta sẽ thử p = 3 và q = 2. Khi đó, p + q = 3 + 2 = 5 là số nguyên tố và p - q = 3 - 2 = 1 không là số nguyên tố. Không thoả mãn yêu cầu.
- Tiếp theo, kiểm tra số nguyên tố thứ hai là 3. Ta sẽ thử p = 5 và q = 3. Khi đó, p + q = 5 + 3 = 8 không là số nguyên tố. Không thoả mãn yêu cầu.
- Tiếp tục kiểm tra các số nguyên tố tiếp theo. Cứ tiếp tục thử cho đến khi tìm được hai số thoả mãn yêu cầu.
Lưu ý rằng việc tìm hai số nguyên tố p và q thoả mãn yêu cầu là một vấn đề tương đối phức tạp và không có một cách giải đơn giản. Ta cần kiểm tra và thử nghiệm để tìm được kết quả.

Bài 1:
Vì ƯCLN(a,b)=45 nên đặt $a=45x, b=45y$ với $x,y$ là 2 số tự nhiên nguyên tố cùng nhau.
Ta có:
$a+b=810$
$45x+45y=810$
$45(x+y)=810$
$x+y=810:45=18$
Do $(x,y)=1$ nên $x,y$ có thể nhận các giá trị là: $(1,17), (5,13), (7,11), (11,7), (13,5), (17,1)$
$\Rightarrow (a,b)=(45,765), (225, 535), (315, 495), (495, 315), (535,225), (765,45)$
Bài 2:
Nếu $p,q$ cùng là số nguyên tố lẻ thì $p+q, p-q$ chẵn. Mà $p-q, p+q$ là snt nên:
$\Rightarrow p+q=2, p-q=2$
$\Rightarrow p=2, q=0$ (vô lý)
Vậy trong 2 số $p,q$ sẽ có 1 số chẵn và 1 số lẻ. Mà $p> q$ nên $p$ là số nguyên tố lẻ còn $q$ là snt chẵn ($q=2$)
Ta cần tìm $p$ nguyên tố sao cho $p+2$ và $p-2$ đều là snt.
Nếu $p\vdots 3$ thì $p=3$. Khi đó $p-2=1$ không là snt (loại)
Nếu $p$ chia $3$ dư $1$ thì $p+2\vdots 3$. Mà $p+2>3$ nên không thể là snt (loại)
Nếu $p$ chia $3$ dư $2$ thì $p-2\vdots 3$
$\Rightarrow p-2=3$
$\Rightarrow p=5$. Khi đó: $p+2=7, p-2=3$ đều là snt (thỏa mãn)
Vậy $p=5,q=2$

a) Vì nên (n + 1) ∈ Ư(6) = {1; 2; 3; 6}
Ta có bảng sau:
n + 1 | 1 | 2 | 3 | 6 |
n | 0 | 1 | 2 | 5 |
Vì n là số tự nhiên nên n ∈ {0; 1; 2; 5}
Vậy n ∈ {0; 1; 2; 5}.
b) Gọi x = 23.3a và y = 2b.35
Ta có tích của hai số là tích của ƯCLN và BCNN của hai số đó.
Ta có: x. y = ƯCLN(x, y). BCNN(x, y)
Vì ước chung lớn nhất của hai số là và bội chung nhỏ nhất của hai số là 23.36.
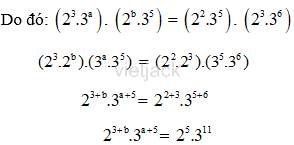
Vì thế 3 + b = 5. Suy ra b = 5 – 3 = 2
a + 5 = 11. Suy ra a = 11 – 5 = 6
Vậy a = 6; b = 2.
Gọi x = 23.3a và y = 2b.35
Ta có: x. y = ƯCLN(x, y). BCNN(x, y)
Vì ước chung lớn nhất của hai số là 22.35 và bội chung nhỏ nhất của hai số là 23.36
Ta được x.y= 22.35.23.36=22.23.35.36=25.31122.35.23.36=22.23.35.36=25.311
Mà xy =23+b.3a+523+b.3a+5
Ta được 5=3+b và 11=a+5
Vậy b=2 và a=6

a: \(n+1\in\left\{1;2;3;6\right\}\)
hay \(n\in\left\{0;1;2;5\right\}\)

a: \(\Leftrightarrow n+1\in\left\{1;2;3;6\right\}\)
hay \(n\in\left\{0;1;2;5\right\}\)
a) \(3x+8=3x+3+5=3\left(x+1\right)+5⋮\left(x+1\right)\)
\(\Leftrightarrow5⋮\left(x+1\right)\)mà \(x\)là số tự nhiên nên \(x+1\inƯ\left(5\right)=\left\{1,5\right\}\)
\(\Leftrightarrow x\in\left\{0,4\right\}\).
b) Do \(\left(a,b\right)=9\)nên ta đặt \(a=9m,b=9n,\left(m,n\right)=1\).
\(a+b=9m+9n=9\left(m+n\right)=45\Leftrightarrow m+n=5\)
Ta có bảng giá trị: