
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Áp dụng quy tắc chia hai căn bậc hai, hãy tính :
a) 2300−−−−√23−−√ = \(\sqrt{\dfrac{2300}{23}}\) = \(\sqrt{100}\) = 10
b) 12,5−−−−√0,5−−−√ = \(\sqrt{\dfrac{12,5}{0,5}}\) = \(\sqrt{25}\) = 5
c) 192−−−√12−−√ = \(\sqrt{\dfrac{192}{12}}\) = \(\sqrt{16}\) = 4
d) 6–√150−−−√ = \(\sqrt{\dfrac{6}{150}}\) = \(\sqrt{\dfrac{1}{25}}\) = \(\dfrac{1}{5}\)


\(3,\dfrac{\sqrt{9+6\sqrt{2}}}{\sqrt{3}}\)
\(=\dfrac{\sqrt{3\left(3+2\sqrt{2}\right)}}{\sqrt{3}}\)
\(=\dfrac{\sqrt{3}.\sqrt{3+2\sqrt{2}}}{\sqrt{3}}\)
\(=\sqrt{3+2\sqrt{2}}\)
\(=\sqrt{\sqrt{2^2}+2\sqrt{2}+1}\)
\(=\sqrt{\left(\sqrt{2}+1\right)^2}\)
\(=\left|\sqrt{2}+1\right|=\sqrt{2}+1\)
\(4,\sqrt{2+\sqrt{3}}:\sqrt{\dfrac{1}{2}}\)
\(=\sqrt{2+\sqrt{3}}:\dfrac{1}{\sqrt{2}}\)
\(=\sqrt{2+\sqrt{3}}.\sqrt{2}\)
\(=\sqrt{4+2\sqrt{3}}\)
\(=\sqrt{\sqrt{3^2}+2\sqrt{3}+1}\)
\(=\sqrt{\left(\sqrt{3}+1\right)}^2\)
\(=\left|\sqrt{3}+1\right|=\sqrt{3}+1\)
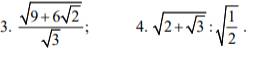 áp dụng quy tắc chia căn bậc hai, hãy tính
áp dụng quy tắc chia căn bậc hai, hãy tính
192 12 = 192 12 = 16 = 4