K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
VV
1
11 tháng 12 2021
x + 6 chia hết cho x + 3
=> x + 3 + 3 chia hết cho x + 3
=> 3 chia hết cho x + 3
=> (x + 3) \(\in\) Ư(3)
=> (x + 3) \(\in\) {-3; -1; 1; 3}
=> x \(\in\) {-6; -4; -2; 0}
22 tháng 12 2017
Trong toán học, số nguyên bao gồm các số nguyêndương (1, 2, 3,…), các số nguyên âm (−1, −2, −3,...) và số 0. ...
DA
1
19 tháng 8 2021
\(2S=3^{31}-1=3^{28}.3^3-1=\left(...1\right).27-1=\left(.....7\right)-1=\left(...6\right)\)
\(\Rightarrow S=\left(...3\right)\)
Tận cùng bằng 3 nhé e
19 tháng 8 2021
3^0 có tận cùng là 1.
3^1 có tận cùng là 3.
3^2 có tận cùng là 9.
3^3 có tận cùng là 7.
3^4 có tận cùng là 1.
................................
3S = ( 3^1+3^2+3^3+......+3^31 )
3S-S = ( 3^1+3^2+3^3+......+3^31 ) - ( 3^0+3^1+3^2+......+3^30 )
2S = 2^31-1
2^31 có tận cùng là 1. ( theo như công thức đã nêu trên )
=> 2S có tận cùng là 0.
2S-S = 2S : 2
=> S có tận cùng là 5 vì ....0 : 2 bằng 5.
LH
14 tháng 5 2021
Nếu là dấu cộng thì bạn phải trừ nếu là dấu trừ thi bạn phải cộng lời giải đó
KD
4
25 tháng 3 2022
\(x=\dfrac{4}{27}-\dfrac{2}{3}\)
\(x=-\dfrac{14}{27}\)
PT
1
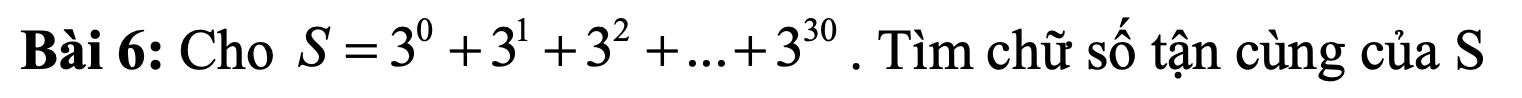
1: =>-9/3<x<8/5+9/5=17/5
=>-3<x<17/5
=>\(x\in\left\{-2;-1;0;1;2;3\right\}\)
2: =>-8/20<x/20<1/12
=>-24/60<3x/60<5/60
=>-24<3x<5
=>\(3x\in\left\{-21;-18;...;0;3\right\}\)
=>\(x\in\left\{-7;-6;...;0;1\right\}\)
3: -1/3<x/24<-1/4
=>-8/24<x/24<-6/24
=>-8<x<-6
=>x=-7
4: