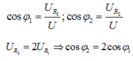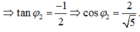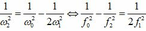Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn D
Z 1 = R 2 + Z L - Z C 2 Z 2 = R 2 + Z L 2
Khi UR tăng lên hai lần
⇒ Z 1 = 2 Z 2 ⇒ Z L - Z C 2 = 4 Z L 2 ⇒ Z C = 3 Z L * tan φ 1 = Z L - Z C R tan φ 2 = Z L R
I1 và I2 vuông pha với nhau nên
tan φ 1 × tan φ 2 = - 1 ⇔ Z L - Z C R × Z L R = - 1 * *
Từ (*) và (**) ta có Z L = R 2
Do đó :
cos φ 1 = R Z 1 = R R 2 + R 2 - 3 R 2 2 = 1 3

Đáp án B
Phương pháp giản đồ vecto.
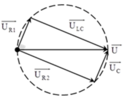
+ Vì u R luôn vuông pha với u L C => đầu mút vecto u R luôn nằm trên đường tròn nhận U là đường kính.
+ Biểu diễn cho hai trường hợp, từ hình vẽ, ta có u C = u R L = 1 (ta chuẩn hóa bằng 1)
Hệ số công suất của mạch lúc sau: 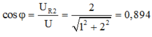

Ta có: φ 1 − φ 2 = π 2 ⇒ tan φ 1 tan φ 2 = − 1 ⇔ Z L − Z C R Z L R = − 1
Chuẩn hóa R = 1 ⇒ Z L − Z C = − 1 Z L
U R 2 = 2 U R 1 ⇔ Z 1 = 2 Z 2 ⇔ 1 + Z L − Z C 2 = 4 + 4 Z L 2
Thay Z L − Z C = − 1 Z L ta thu được
1 + R Z L 2 4 = 4 + 4 Z L 2 ⇒ 4 Z L 4 + 3 Z L 2 − 1 = 0 ⇒ Z L = 1 2
→ Vậy hệ số công suất của mạch cos φ = 1 1 2 + 1 2 2 = 2 5
Đáp án A

Điện áp hiệu dụng của mạch: \(U=\sqrt{15^2+\left(20-40\right)^2}=25V\)
\(\frac{Z_L}{Z_C}=\frac{U_L}{U_C}=\frac{1}{2}\)
\(\Rightarrow\frac{\omega L}{\frac{1}{\omega C}}=\frac{1}{2}\Rightarrow\omega^2LC=\frac{1}{2}\)\(\Rightarrow\frac{1}{\sqrt{LC}}=\sqrt{2}\omega\)
Để có cộng hưởng điện thì \(\omega_0=\frac{1}{\sqrt{LC}}=\sqrt{2}\omega\)
\(\Rightarrow f_0=\sqrt{2}f=50\sqrt{2}\)
Vì cộng hưởng nên: \(U=U_R=25V\)
Chọn đáp án B.

Đáp án C
Khi ω = ω1 thì 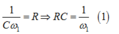
Khi ω = ω2 thì 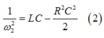
Khi ω = ω0 thì
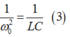
Thay (1) và (3) và (2) ta thu được 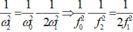

Ta có giản đồ véc tơ:
U U U R MB phi
Ta có \(\sin\varphi=\frac{U_{MB}}{U}\)
nên: \(\sin\varphi_1=\frac{U_{MB1}}{U}\)(*)
\(\sin\varphi_2=\frac{U_{MB2}}{U}\)
Mà \(U_{MB2}=2\sqrt{2}U_{MB1}\) nên: \(\sin\varphi_2=2\sqrt{2}\sin\varphi_1\)
Mặt khác: Do \(\left|\varphi_1\right|+\left|\varphi_2\right|=90^0\) nên \(\sin\varphi_2=\cos\varphi_1\), lại có: \(\sin^2+\cos^2=1\)
Giải ra ta đc: \(\sin\varphi_1=\frac{1}{3}\)
Thay vào (*) ta đc: \(U_{MB}=\frac{U}{3}=50V\)
\(\cos\varphi_2=\sin\varphi_1=\frac{1}{3}\)