
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


bài giải
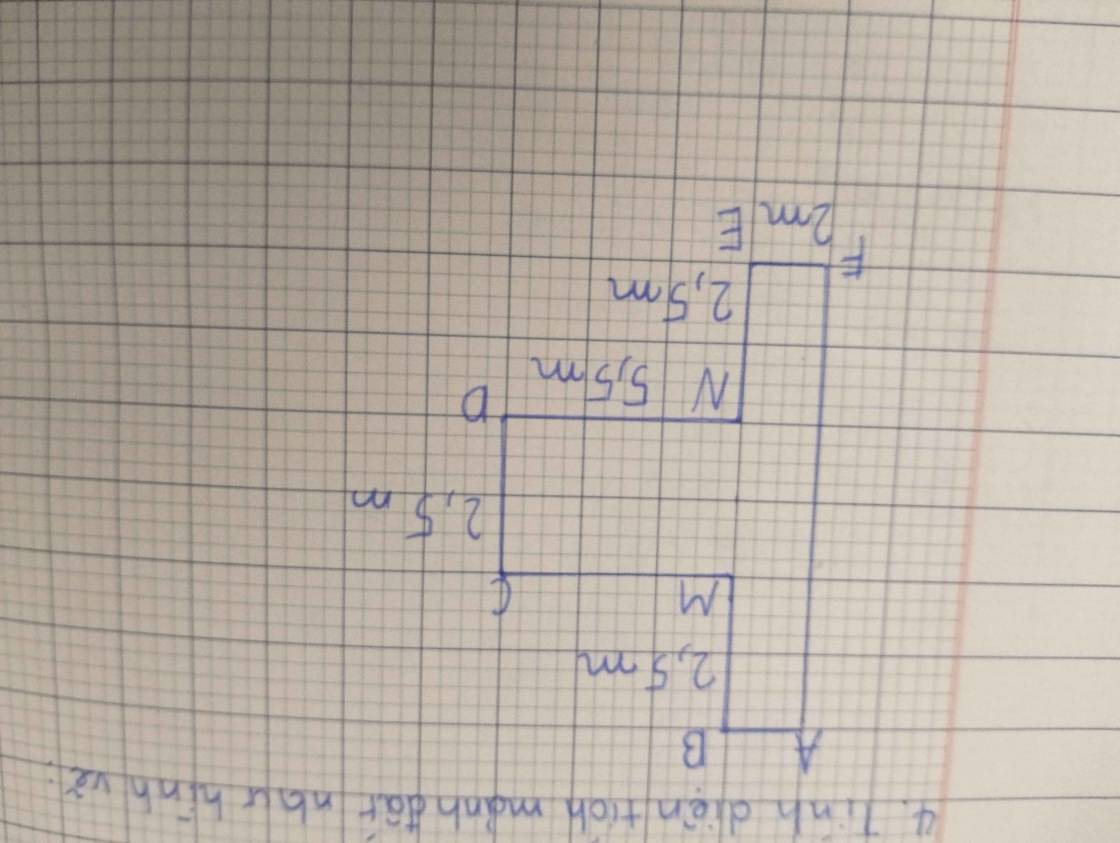
diện tích hình đó là:
( 2,5 x 3 ) x 2 + 5,5 x 2,5 = 28,75 ( m2 )
đáp số : 28,75 m2.
cố lắm mới nhìn đc cái hình ngược :)
sắp trẹo cổ r

diện tích tôn để là cái thùng là:
( 60 + 40 ) x 2 x 80 + 60 x 40 = 18400 ( dm2 )
đáp số: 18400 dm2.

Câu 3:
Cạnh đáy kéo dài thêm 5m thì diện tích tăng:
(5 x 12) : 2 = 30 (m2)
Đ.số:.....
Câu 2:
Chiều cao mảnh đất:
25,48 x 2 : 2,8 = 18,2 (m)
Cạnh đáy mảnh đất:
42,7 x 2 : 2,8 = 30,5 (m)
Diện tích mảnh đất hình tam giác đã cho là:
(30,5 x 18,2) : 2 = 277,55 (m2)
Đ.số:......

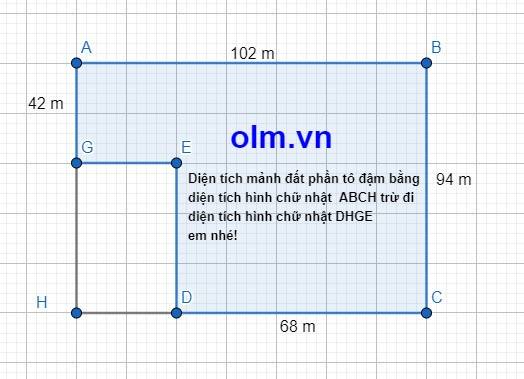
Diện tích mảnh đất bằng diện tích hình chữ nhật ABCH trừ đi diện tích hinh chữ nhật DHGE em nhé.
Diện tích hình chữ nhật ABCH là:
102 x 94 = 9588 (m2)
Diện tích hình chữ nhật DHGE là:
(94 - 42) x (102 - 68) = 1768 (m2)
Diện tích mảnh đất hình là:
9588 - 1768 = 7820 (m2)
Đs...

Ta có sơ đồ:
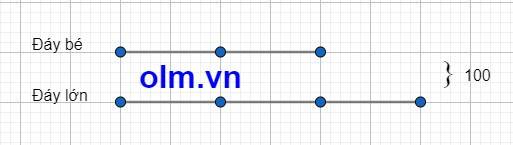
Theo sơ đồ ta có:
Đáy bé của mảnh đất hình thang là: 100 : (2 + 3) x 2 = 40 (m)
Chiều cao của mảnh đất hình thang là: 40 + 20 = 60 (m)
Diện tích của mảnh đất hình thang là: 100 x 60 : 2 = 3000 (m2)
Mỗi mét vuông thu được số ki-lô-gam táo là: 70 : 100 = \(\dfrac{7}{10}\) (kg)
Cả mảnh đất thu được số ki-lô-gam táo là: \(\dfrac{7}{10}\) x 3000 = 2100 (kg)
2100 kg = 21 tạ
Đs...

Độ dài đáy bé của mảnh vườn hình thang là:
16 x 75 : 100 = 12 (m)
Diện tích mảnh vườn hình thang là:
(16 + 12) x 8 : 2 = 112 (m2)
b; Diện tích trồng rau so với diện tích mảnh vườn chiếm số phần trăm là:
39,2 : 112 = 0,35
0,35 = 35%
Đáp số: 35%

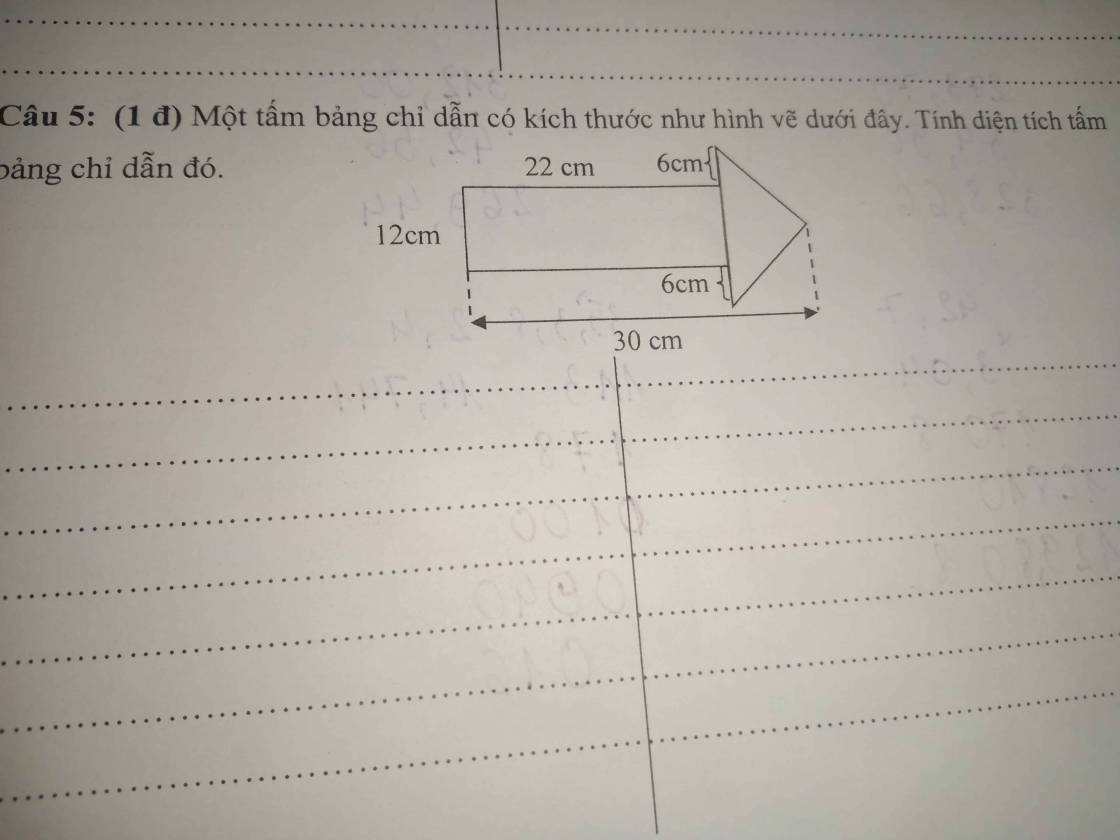
diện tích HCN là:
22 x 12 = 264 (cm2)
chiều cao của hình tam giác là:
30 - 22 = 8 (cm)
độ dài đáy của hình tam giác là:
6 + 12 + 6 = 24 (cm)
diện tích hình tam giác là:
\(\dfrac{24\times8}{2}=96\left(cm^2\right)\)
diện tích tấm bảng chỉ dẫn là:
96 + 264 = 360 (cm2)
đáp số: 360 (cm2)

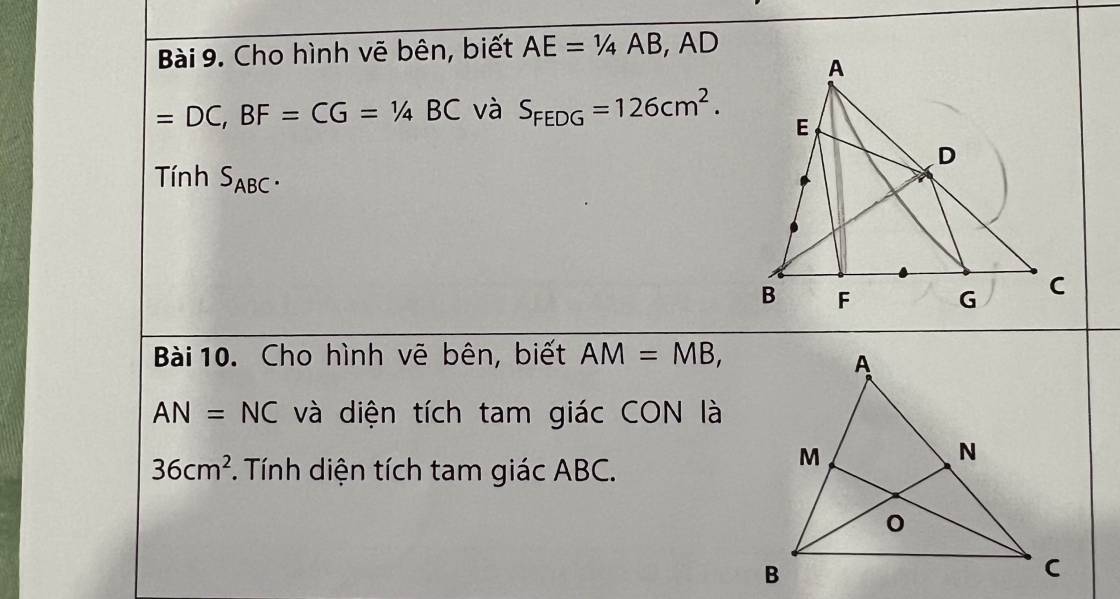
a; N trên AC nên A; C; N thẳng hàng làm sao thành tam giác ANC được em?
b; AB = AM + BM = AM + AM \(\times\) 2 = AM \(\times\) 3
SABN = SAMN \(\times\) 3 (vì hai tam giác có chung chiều cao hạ từ đỉnh N xuống đáy AB và AB = AM \(\times\) 3)
AC = AN + NC = AN + AN \(\times\) 2 = AN \(\times\) 3
SACB = SANB \(\times\) 3 (Vì hai tam giác có chung chiều cao hạ từ đỉnh B xuống đáy AC và AC = AN \(\times\) 3)
SABC = SAMN \(\times\) 3 \(\times\) 3 = SAMN \(\times\) 9 = 12 \(\times\) 9 = 108 (cm2)


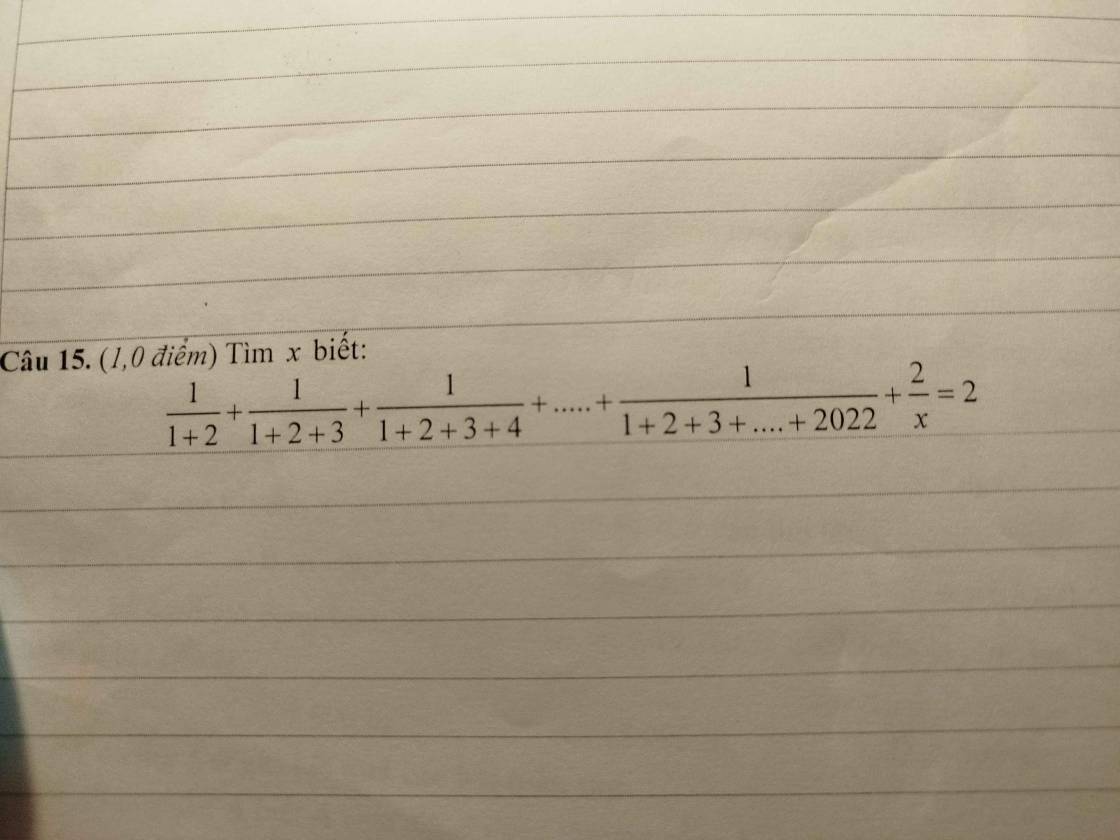






\(\dfrac{1}{1+2}+\dfrac{1}{1+2+3}+...+\dfrac{1}{1+2+3+...+2022}+\dfrac{2}{x}=2\)
=>\(\dfrac{1}{2\text{x}\dfrac{3}{2}}+\dfrac{1}{3\text{x}\dfrac{4}{2}}+...+\dfrac{1}{2022\text{x}\dfrac{2023}{2}}+\dfrac{2}{x}=2\)
=>\(\dfrac{2}{2\text{x}3}+\dfrac{2}{3\text{x}4}+...+\dfrac{2}{2022\text{x}2023}+\dfrac{2}{x}=2\)
=>\(\dfrac{1}{2\text{x}3}+\dfrac{1}{3\text{x}4}+...+\dfrac{1}{2022\text{x}2023}+\dfrac{1}{x}=1\)
=>\(\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{2022}-\dfrac{1}{2023}+\dfrac{1}{x}=1\)
=>\(\dfrac{1}{2}-\dfrac{1}{2023}+\dfrac{1}{x}=1\)
=>\(\dfrac{1}{x}=1-\dfrac{1}{2}+\dfrac{1}{2023}=\dfrac{1}{2}+\dfrac{1}{2023}=\dfrac{2025}{4046}\)
=>\(x=\dfrac{4046}{2025}\)
\(\dfrac{1}{1+2}\) + \(\dfrac{1}{1+2+3}\) + ... + \(\dfrac{1}{1+2+3+4+...+2022}\) + \(\dfrac{2}{x}\) = 2
\(\dfrac{1}{\left(1+2\right)\times2:2}\) + \(\dfrac{1}{\left(1+3\right)\times3:2}\)+ ... + \(\dfrac{1}{\left(1+2022\right)\times2022:2}\) + \(\dfrac{2}{x}\) = 2
\(\dfrac{2}{2\times3}\) + \(\dfrac{2}{3\times4}\) + ... + \(\dfrac{2}{2022\times2023}\) + \(\dfrac{2}{x}\) = 2
2 x (\(\dfrac{1}{2\times3}\) + \(\dfrac{1}{3\times4}\) + ... + \(\dfrac{1}{2022\times2023}\)) + \(\dfrac{2}{x}\) = 2
2 \(\times\) (\(\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{2022}-\dfrac{1}{2023}\)) + \(\dfrac{2}{x}\) = 2
2 \(\times\) (\(\dfrac{1}{2}\) - \(\dfrac{1}{2023}\)) + \(\dfrac{2}{x}\) = 2
2 x \(\dfrac{1011}{2023}\) + \(\dfrac{2}{x}\) = 2
\(\dfrac{2021}{2023}\) + \(\dfrac{2}{x}\) = 2
\(\dfrac{2}{x}\) = 2 - \(\dfrac{2021}{2023}\)
\(\dfrac{2}{x}\) = \(\dfrac{2025}{2023}\)
\(x\) = 2 : \(\dfrac{2025}{2023}\)
\(x\) = \(\dfrac{4046}{2025}\)