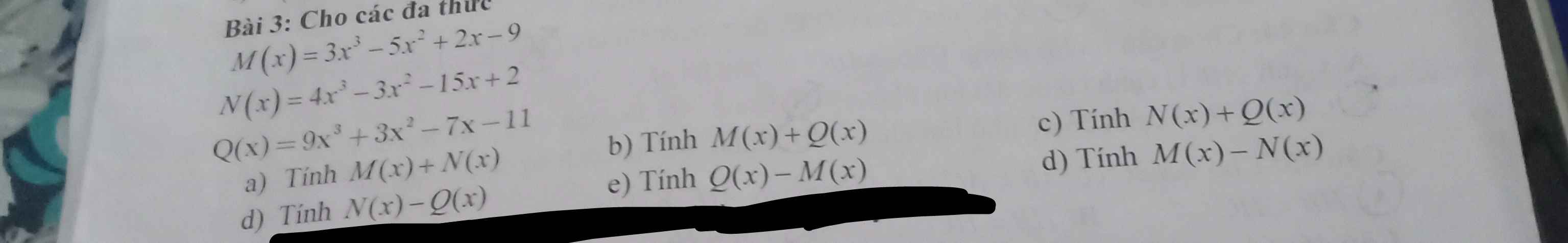Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\left(x-7\right)^{x+1}-\left(x-7\right)^{16}=0\)
\(\Leftrightarrow\left(x-7\right)^{16}.\left(x-7\right)^{x-15}-\left(x-7\right)^{16}=0\)
\(\Leftrightarrow\left(x-7\right)^{16}\left[\left(x-7\right)^{x-15}-1\right]=0\)
\(\Leftrightarrow\orbr{\begin{cases}\left(x-7\right)^{16}=0\\\left(x-7\right)^{x-15}=1\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}x-7=0\\\left(x-7\right)^{x-15}=1^{x-15};\left(x-7\right)^{x-15}=\left(x-7\right)^0\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}x=7\\x-7=1;x-15=0\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}x=7\\x=8;x=15\end{cases}}\)
Vậy \(x\in\left\{7;8;15\right\}\)
P/s: Thay cái ngoặc có 2 nhánh thành ngoặc 3 nhánh cho nó đẹp :))

a: M(x)+N(x)=7x^3-8x^2-13x-7
b: M(x)+Q(x)=12x^3-2x^2-5x-20
c: N(x)+Q(x)=13x^3-22x-9
d: N(x)-Q(x)=-5x^3-6x^2-8x+13
e: Q(x)-M(x)=6x^3+8x^2-9x-2

Ta có:M là trung điểm của BC=>BM=MC
Mà IM=\(\frac{BM}{2}\)(I là trung điểm của BM)
=>IM\(=\frac{MC}{2}\)(1)
Vì IA=IE(gt)
=>CI là đường trung tuyến ứng với cạnh AE của \(\Delta AEC\)(2)
Từ (1),(2)=>M là giao điềm của 3 đường trung tuyến của \(\Delta AEC\)
Vì N là trung điểm của EC(gt)
=>AN là đường trung tuyến ứng với cạnh EC của \(\Delta AEC\)
Xét \(\Delta AEC\)có:
AN là đường trung tuyến ứng với cạnh EC
M là giao điểm của 3 đường trung tuyến
=>A,M,N thẳng hàng
Mình ko biết vẽ hình ở đâu nên ko vẽ mà chỉ trình bày thôi.
Bài giải
*Ta có:
+ M là td của BC (gt) => MB=MC(t/c)
+ I là td của BM (gt) => IM= IB(t/c)
mà MB=MC(cmt) => IM=IB=1/2 MC
=> M là trọng tâm ( t/c trọng tâm )
*Xét tam giác AEC có :
I là td của AE (gt) =>CI là trung tuyến
N là td của EC (gt) =>AN là trung tuyến
mà M là trọng tâm (cmt) => M thuộc AN
=> A,M,N thẳng hàng (dpcm)

Tôi thấy bài này nó cứ sai sai
Ở chỗ \(\frac{1}{99.97}-\frac{1}{97.95}\)í
\(\frac{1}{97.95}>\frac{1}{99.97}\)mà ông Thám Tử THCS Nguyễn Hiếu CTV
violympic cho sai đề :
Đề đúng là tính : \(A=\frac{1}{99.97}-\frac{1}{97.95}-\frac{1}{95.53}-....-\frac{1}{5.3}-\frac{1}{3.1}\)
Làm theo đề đúng !! ok
Ta có : \(A=\frac{1}{99.97}-\left(\frac{1}{97.95}+\frac{1}{95.53}+....+\frac{1}{5.3}+\frac{1}{3.1}\right)\)
\(=\frac{1}{99.97}-\frac{1}{2}\left(1-\frac{1}{3}+\frac{1}{3}-\frac{1}{5}+....+\frac{1}{95}-\frac{1}{97}\right)\)
\(=\frac{1}{99.97}-\frac{1}{2}\left(1-\frac{1}{97}\right)=\frac{1}{99.97}-\frac{48}{97}=-\frac{4751}{9603}\)

Đặt A = 1 +3 +5 +...+(2n-1)
Số số hạng của A là : [(2n-1)-1]:2 +1 = n
Tổng A = [(2n-1)+1]xn:2=n2
=> n2=169
=>n2=132
=>n=13

GTNN (A)=3178+2017 khi x=0 ko co GTLN
GTLN(b)=2017 khi x=-3 va y=5 khong co GTNN
GTNN(c)=2018 khi x=-1 va y=5 khong co GTLN
neu can giai thich thi h
ko thi thoi
em cũng muốn làm phước giúp chị lắm chứ nhưng em mới ở lớp 6 thui