K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
6 tháng 3 2023
a: MA=MC
OA=OC
=>OM là trung trực của AC
=>OM vuông góc AC
Vì góc AHO+góc AMO=180 độ
=>AHOM là tứ giác nội tiếp
6 tháng 3 2023
10: =>1/2x=3/4 và x+y=2
=>x=3/4*2=3/2 và y=1/2
11:=>4x+5y=3 và 4x-12y=20
=>17y=-17 và x-3y=5
=>y=-1 và x=3y+5=-3+5=2
12: =>7x-2y=1 và 6x+2y=12
=>13x=13 và 3x+y=6
=>x=1 và y=3
13:=>2/x=1 và 1/x-1/y=1/5
=>x=2 và 1/y=1/2-1/5=3/10
=>y=10/3 và x=2
14: =>12/x-16/y=8 và 12/x-15/y=9
=>-1/y=-1 và 4/x-5/y=3
=>y=1 và 4/x=3+5=8
=>x=1/2 và y=1
8 tháng 1 2022
a: Xét (O) có
OH là một phần đường kính
AD là dây
OH⊥AD tại H
Do đó: H là trung điểm của AD
b: Xét ΔOAC vuông tại A có AH là đường cao
nen \(OH\cdot OC=OA^2=R^2\)
d: Xét ΔOAC và ΔODC có
OA=OD
\(\widehat{AOC}=\widehat{DOC}\)
OC chung
Do đó: ΔOAC=ΔODC
Suy ra: \(\widehat{OAC}=\widehat{ODC}=90^0\)
hay CD là tiếp tuyến của (O)
27 tháng 12 2021
\(b,\Leftrightarrow\left\{{}\begin{matrix}m+1=3\\m-3\ne-3\end{matrix}\right.\Leftrightarrow m=2\\ c,\text{PT giao Ox tại hoành độ 3: }\\ x=-3;y=0\Leftrightarrow\left(m+1\right)\left(-3\right)+m-3=0\\ \Leftrightarrow-2m-6=0\Leftrightarrow m=-3\)
10 tháng 1 2022
a: \(-m^2-4m-7=-\left(m^2+4m+7\right)=-\left(m+2\right)^2-3< 0\)
=>Hàm số luôn nghịch biến khi x>0 và đồng biến khi x<0
b: Thay x=-2 và y=-16 vào (P), ta được:
\(4\left(-m^2-4m-7\right)=-16\)
\(\Leftrightarrow m^2+4m+7=4\)
=>(m+1)(m+3)=0
=>m=-1 hoặc m=-3
12 tháng 1 2022
a: Thay \(x=-\sqrt{6};y=6\) vào (P), ta đc:
\(6\left(n-1\right)^2=6\)
=>\(\left(n-1\right)^2=1\)
\(\Leftrightarrow\left[{}\begin{matrix}n-1=1\\n-1=-1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}n=2\\n=0\end{matrix}\right.\)
Vậy: (P): y=x2
II: Thay x=2 vào (P), ta được:
\(y=2^2=4\)
Vậy: Điểm cần tìm có tọa độ là (2;4)
16 tháng 1 2022
a: Để phương trình có hai nghiệm phân biệt thì
\(1^2-4\cdot1\left(m-2\right)>0\)
=>4(m-2)<1
=>m-2<1/4
hay m<9/4
b: \(\Leftrightarrow3^2-4\cdot\left(-2\right)\left(m-3\right)>0\)
=>9+8(m-3)>0
=>9+8m-24>0
=>8m-15>0
hay m>15/8
8 tháng 1 2022
a) Thay x = 9 vào B ta có
\(B=\dfrac{9+\sqrt{9}+1}{\sqrt{9}+2}=\dfrac{13}{5}\)
8 tháng 1 2022
a: Thay x=9 vào B, ta được:
\(B=\dfrac{9+3+1}{3+2}=\dfrac{13}{5}\)
b: \(A=\dfrac{2x+4+x+\sqrt{x}-2-2x-2\sqrt{x}-2}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\)
\(=\dfrac{x-\sqrt{x}}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}=\dfrac{\sqrt{x}}{x+\sqrt{x}+1}\)
d: \(P=A\cdot B=\dfrac{\sqrt{x}}{x+\sqrt{x}+1}\cdot\dfrac{x+\sqrt{x}+1}{\sqrt{x}+2}=\dfrac{\sqrt{x}}{\sqrt{x}+2}\)
Để P nguyên thì \(\sqrt{x}+2=2\)
hay x=0
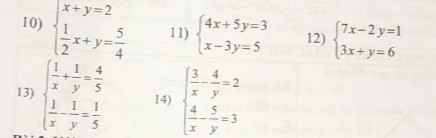
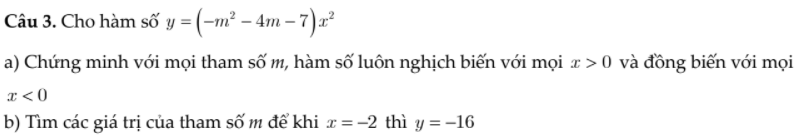
a) Gọi phương trình đường thẳng (từ đây tớ viết tắt là ptđt cho gọn) của (d) là \(\left(d\right):y=ax+b\)
Đường thẳng (d) đi qua A(-1;2) nên ta thay \(x=-1;y=2\)vào ptđt (d), ta có: \(2=-a+b\Rightarrow b=a+2\)(1)
(d) đi qua B(1;3) nên thay \(x=1;y=3\)vào ptđt (d), ta có: \(3=a+b\Rightarrow b=3-a\)(2)
Từ (1) và (2) \(\Rightarrow a+2=3-a\Rightarrow a=\frac{1}{2}\)\(\Rightarrow b=a+2=\frac{1}{2}+2=\frac{5}{2}\)
Vậy ptđt (d) đi qua A(-1;2) và B(1;3) là \(\left(d\right):y=\frac{1}{2}x+\frac{5}{2}\)
b) Gọi ptđt (d1) là \(\left(d_1\right):y=a_1x+b_1\)
Vì \(\left(d_1\right)\perp\left(d\right)\)mà đường thẳng (d) chính là đường thẳng \(\left(d\right):y=\frac{1}{2}x+\frac{5}{2}\)nên \(\frac{1}{2}.a_1=-1\Rightarrow a_1=\frac{-1}{\frac{1}{2}}=-2\)
Mà (d1) đi qua C(2;3) nên thay \(x=2;y=3\)vào ptđt (d1), ta có:
\(3=-2.2+b\Rightarrow b=7\)
Vậy ptđt (d1) là \(\left(d_1\right):y=-2x+7\)
c) Phương trình hoành độ giao điểm của (d) và (d1) là \(\frac{1}{2}x+\frac{5}{2}=-2x+7\Leftrightarrow\frac{1}{2}x+2x=7-\frac{5}{2}\Leftrightarrow\frac{5}{2}x=\frac{9}{2}\Leftrightarrow x=\frac{9}{5}\)
\(\Rightarrow y=-2x+7=-2.\frac{9}{5}+7=\frac{17}{5}\)
Vậy tọa độ điểm D là \(D\left(\frac{9}{5};\frac{17}{5}\right)\)
d) Vì (d2) đi qua D nên thay \(x=\frac{9}{5};y=\frac{17}{5}\)vào ptđt (d2), ta có:
\(\frac{17}{5}=\frac{9}{5}\left(m-1\right)+m+3\)
Rồi giải phương trình trên và dễ dàng tìm được \(m=\frac{11}{14}\)