
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(a,\left|x+3,4\right|+\left|x+2,4\right|+\left|x+7,2\right|=4x\)
\(\left|x+3,4\right|\ge0;\left|x+2,4\right|\ge0;\left|x+7,2\right|\ge0\)
\(< =>\left|x+3,4\right|+\left|x+2,4\right|+\left|x+7,2\right|>0\)
\(< =>4x>0\)
\(x>0\)
\(\hept{\begin{cases}\left|x+3,4\right|=x+3,4\\\left|x+2,4\right|=x+2,4\\\left|x+7,2\right|=x+7,2\end{cases}}\)
\(x+3,4+x+2,4+x+7,2=4x\)
\(x=13\left(TM\right)\)
\(b,3^{n+3}+3^{n+1}+2^{n+3}+2^{n+2}\)
\(3^n.27+3^n.3+2^n.8+2^n.4\)
\(3^n.30+2^n.12\)
\(\hept{\begin{cases}3^n.30⋮6\\2^n.12⋮6\end{cases}}\)
\(< =>3^n.30+2^n.12⋮6< =>VP⋮6\)



Điều kiện:
\(x-1\ne0\Rightarrow x\ne1\)
\(x^3+x\ne0\Leftrightarrow x\ne0\)

52 + 122 =132 => tg vuong
Sabc = 12.5/2 = 30cm2
( toán violympic cho rất thông minh, mới nhìn là mk phát hiện ra r , thui mk đi học đây)
Tam giác ABC có 3 cạnh của tam giác ứng với định lí Py-ta-go=> ABC là tam giác vuông
\(S_{ABC}=\frac{5.12}{2}=30cm^2\)

Xét tứ giác ABEC có
AB//EC
AC//BE
Do đó: ABEC là hình bình hành
Suy ra: AC=BE
mà AC=BD
nên BE=BD
hay ΔBED cân tại B

ta có : CK vuông góc DB (1)
AH vuông góc DB (2)
từ (1),(2) suy ra AH//CK (*)
xét tam giác vuông AHD và tam giác vuông CBK:ta có
góc H=góc K=90
góc ADH=góc CBK(slt)
suy ra 2 tam giác đó bằng nhau
suy ra AH=CK (*')
từ (*),(*') ta có tứ giác AHCK là hình bình hình

Câu 1)\(H=\left(x-y+z\right)^2+\left(z-y\right)^2+2\left(x-y+z\right)\left(y-z\right)\)
\(\Leftrightarrow H=\left(x-y+z+z-y\right)^2\)
\(\Leftrightarrow H=\left(x-2y+2z\right)^2\)
Câu 2: \(Q=2x^2-6x\)
\(\Leftrightarrow Q=2\left(x^2-2.\dfrac{3}{2}.x+\left(\dfrac{3}{2}\right)^2\right)-\dfrac{9}{2}\)
\(\Leftrightarrow Q=2.\left(x-\dfrac{3}{2}\right)^2-\dfrac{9}{2}\ge\dfrac{-9}{2}\)
Min \(Q=\dfrac{-9}{2}\Leftrightarrow x=\dfrac{3}{2}\)
2.
\(a,Q=2x^2-6x=2\left(x^2-3x+\dfrac{9}{4}\right)-\dfrac{9}{2}=2\left(x-\dfrac{3}{2}\right)^2-\dfrac{9}{2}\ge\dfrac{-9}{2}\)Vậy \(Min_Q=\dfrac{-9}{2}\) khi \(x-\dfrac{3}{2}=0\Rightarrow x=\dfrac{3}{2}\)
\(b,M=x^2+y^2-x+6y+10=\left(x^2-x+\dfrac{1}{4}\right)+\left(y^2+6y+9\right)+\dfrac{3}{4}=\left(x-\dfrac{1}{2}\right)^2+\left(y+3\right)^2+\dfrac{3}{4}\ge\dfrac{3}{4}\)
vậy \(Min_M=\dfrac{3}{4}\)khi \(\left[{}\begin{matrix}x-\dfrac{1}{2}=0\\x+3=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=\dfrac{1}{2}\\x=-3\end{matrix}\right.\)
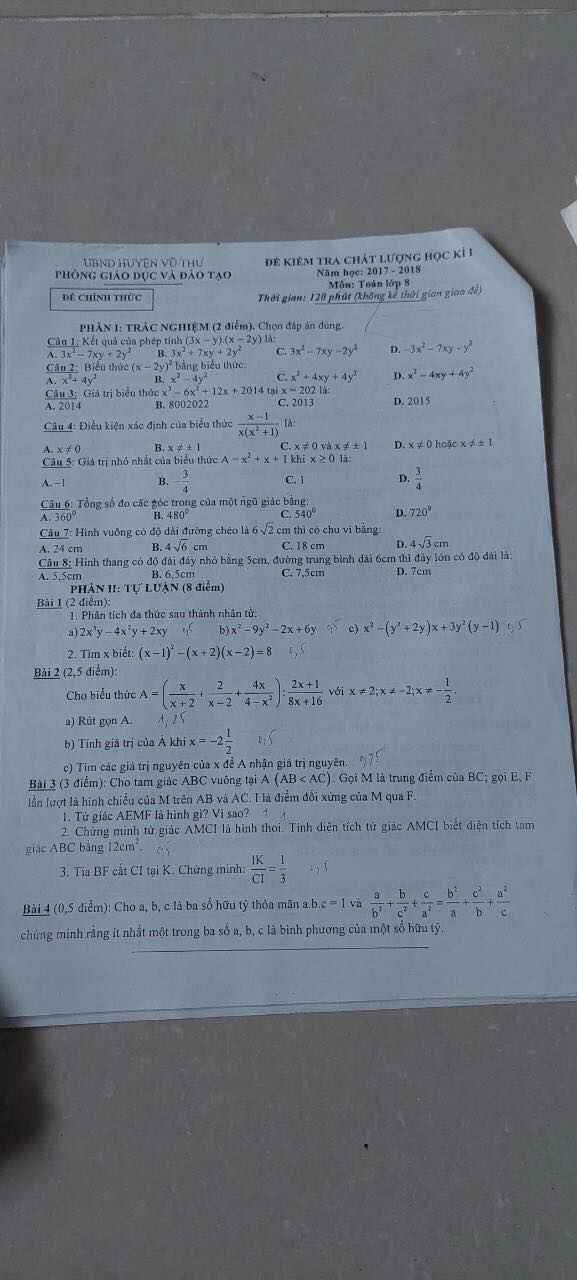



 giúp mik với nha!
giúp mik với nha!

 giúp mk nha mờn nhìu ạk
giúp mk nha mờn nhìu ạk






 giúp mình nha
giúp mình nha