
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1: góc ABO+góc ACO=180 độ
=>OBAC nội tiếp
2: Xét ΔABH và ΔAKB có
góc ABH=góc AKB
góc BAH chung
=>ΔABH đồng dạng với ΔAKB
=>AB/AK=AH/AB
=>AB^2=AK*AH


\(12,ĐK:x,y\ne0\\ HPT\Leftrightarrow\left\{{}\begin{matrix}\dfrac{4}{x}+\dfrac{2}{y}=4\\\dfrac{6}{x}-\dfrac{2}{y}=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{10}{x}=5\\\dfrac{2}{x}+\dfrac{1}{y}=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\\dfrac{1}{y}=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=1\end{matrix}\right.\left(tm\right)\)
\(13,\Leftrightarrow\left\{{}\begin{matrix}3\left(x+1\right)+2\left(x+2y\right)=4\\8\left(x+1\right)-2\left(x+2y\right)=18\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}11\left(x+1\right)=22\\3\left(x+1\right)+2\left(x+2y\right)=4\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=1\\6+2+4y=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=-1\end{matrix}\right.\)
\(14,ĐK:x+y\ne0;y\ne1\\ HPT\Leftrightarrow\left\{{}\begin{matrix}\dfrac{4}{x+y}+\dfrac{1}{y-1}=5\\\dfrac{4}{x+y}-\dfrac{8}{y-1}=-4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{1}{x+y}-\dfrac{2}{y-1}=-1\\\dfrac{9}{y-1}=9\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}\dfrac{1}{x+2}=1\\y=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x+2=1\\y=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-1\\y=2\end{matrix}\right.\left(tm\right)\)
\(15,ĐK:x\ge-1\\ HPT\Leftrightarrow\left\{{}\begin{matrix}2\left(x+y\right)+\sqrt{x+1}=4\\2\left(x+y\right)-6\sqrt{x+1}=-10\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}7\sqrt{x+1}=14\\2\left(x+y\right)+\sqrt{x+1}=4\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=3\left(tm\right)\\6+2y+2=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=3\\y=-2\end{matrix}\right.\left(tm\right)\)
\(16,ĐK:x\ne1;y\ne-2\\ HPT\Leftrightarrow\left\{{}\begin{matrix}\dfrac{3x}{x-1}-\dfrac{2}{y+2}=4\\\dfrac{4x}{x-1}+\dfrac{2}{y+2}=10\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{7x}{x-1}=14\\\dfrac{2x}{x-1}+\dfrac{1}{y+2}=5\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=2\\\dfrac{1}{y+2}=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=-1\end{matrix}\right.\left(tm\right)\)
\(17,ĐK:x\ge0;y\ge1\\ HPT\Leftrightarrow\left\{{}\begin{matrix}\sqrt{x}+2\sqrt{y-1}=5\\8\sqrt{x}-2\sqrt{y-1}=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}9\sqrt{x}=9\\\sqrt{x}+2\sqrt{y-1}=5\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=1\\\sqrt{y-1}=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=5\end{matrix}\right.\)
\(18,\Leftrightarrow\left\{{}\begin{matrix}8x-2\left|y+2\right|=6\\x+2\left|y+2\right|=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}9x=9\\x+2\left|y+2\right|=3\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=1\\\left|y+2\right|=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\\left[{}\begin{matrix}y=-1\\y=-3\end{matrix}\right.\end{matrix}\right.\\ 20,ĐK:y\ne1\\ HPT\Leftrightarrow\left\{{}\begin{matrix}2x+\dfrac{3}{y-1}=5\\12x-\dfrac{3}{y-1}=9\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}14x=14\\2x+\dfrac{3}{y-1}=5\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=1\\\dfrac{3}{y-1}=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=2\end{matrix}\right.\left(tm\right)\)
\(21,ĐK:x\ne-1\\ HPT\Leftrightarrow\left\{{}\begin{matrix}\dfrac{9}{x+1}-6y=-3\\\dfrac{10}{x+1}+6y=22\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{19}{x+1}=19\\\dfrac{3}{x+1}-2y=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\3-2y=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\y=2\end{matrix}\right.\left(tm\right)\)


a: Thay \(x=9+4\sqrt{2}\) vào A, ta được:
\(A=\dfrac{2\sqrt{2}+1+7}{2\sqrt{2}+1-1}=\dfrac{8+2\sqrt{2}}{2\sqrt{2}}=2\sqrt{2}+1\)


\(a,m=3\Leftrightarrow y=2x+2\\ A\left(a;-4\right)\in\left(d\right)\Leftrightarrow2a+2=-4\Leftrightarrow a=-3\)
\(b,\) PT giao Ox của (d) là \(2x+m-1=0\Leftrightarrow x=\dfrac{1-m}{2}\Leftrightarrow M\left(\dfrac{1-m}{2};0\right)\Leftrightarrow OM=\dfrac{\left|1-m\right|}{2}\)
PT giao Oy của (d) là \(x=0\Leftrightarrow y=m-1\Leftrightarrow N\left(0;m-1\right)\Leftrightarrow ON=\left|m-1\right|\)
Để \(S_{OMN}=1\Leftrightarrow\dfrac{1}{2}OM\cdot ON=1\Leftrightarrow OM\cdot ON=2\)
\(\Leftrightarrow\dfrac{\left|\left(1-m\right)\left(m-1\right)\right|}{2}=2\\ \Leftrightarrow\left|-\left(m-1\right)^2\right|=2\\ \Leftrightarrow\left(m-1\right)^2=2\\ \Leftrightarrow\left[{}\begin{matrix}m=1+\sqrt{2}\\m=1-\sqrt{2}\end{matrix}\right.\)

câu 1:
đường thẳng (d) song song với đường thẳng y=3x+1 khi a=3
vậy hệ số góc của đường thẳng (d) song song với đường thẳng y=3x+1 là 3
câu 2:
vì góc tạo bởi đường thẳng (d):y=ax+b(a≠0) với trục Ox là 30o nên
\(a=\tan30^o=\dfrac{1}{\sqrt{3}}=\dfrac{\sqrt{3}}{3}\)
vậy hệ số góc của đường thẳng (d) tạo với trục Ox là\(\dfrac{\sqrt{3}}{3}\)
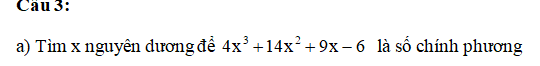

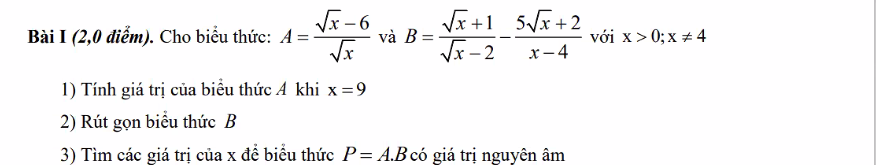

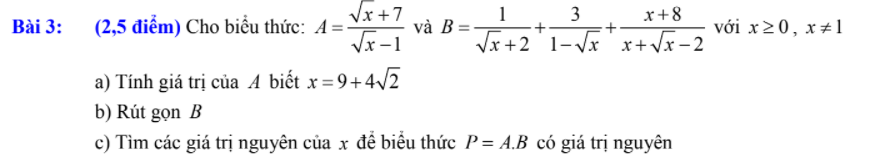 được không ạ, mai em phải nộp rồi, cảm ơn mn nhiều.
được không ạ, mai em phải nộp rồi, cảm ơn mn nhiều. 

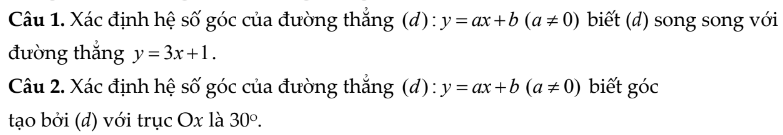

Đặt \(A=4x^3+14x^2+9x-6\)
\(\Leftrightarrow A=\left(x+2\right)\left(4x^2+6x-3\right)\)
Để A là số chính phương thì \(x+2=4x^2+6x-3\) (1) hoặc \(x+2\) và \(4x^2+6x-3\) có dạng chính phương (2)
Giải trường hợp (1) \(\Rightarrow4x^2+5x-5=0\)
\(\Delta=5^2+4\cdot4\cdot5=105>0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{-5+\sqrt{105}}{8}\\x=\dfrac{-5+\sqrt{105}}{8}\end{matrix}\right.\) (loại do cả 2 đều âm KTM đề bài)
Giải trường hợp (2):
Đặt \(\left\{{}\begin{matrix}x+2=a^2\\4x^2+6x-3=b^2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x+2=a^2\\4x\left(x+2\right)-2\left(x+2\right)+1=b^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=a^2-2\\4\left(a^2-2\right)a^2-2a^2+1=b^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=a^2-2\\4a^4-10a^2+1=b^2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=a^2-2\\\left(2a^2-\dfrac{5}{2}\right)^2-\dfrac{21}{4}=b^2\left(3\right)\end{matrix}\right.\)
Giải (3), ta được:
\(\left(4a^2-5\right)^2-21=4b^2\)
\(\Leftrightarrow\left(4a^2-5\right)^2-4b^2=21\)
\(\Leftrightarrow\left(4a^2-5-2b\right)\left(4a^2-5+2b\right)=21\cdot1=1\cdot21=3\cdot7=7\cdot3\)
Với \(\left\{{}\begin{matrix}4a^2-5-2b=1\\4a^2-5+2b=21\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}4a^2-5+2b=21\\b=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}4a^4-10a^2+1=25\\b=5\end{matrix}\right.\)
Đặt \(a^2=t\left(t>0\right)\)\(\Leftrightarrow4t^2-10t-24=0\Leftrightarrow\left[{}\begin{matrix}t=4\left(N\right)\\t=-\dfrac{3}{2}\left(L\right)\end{matrix}\right.\)
\(\Leftrightarrow a^2=4\Leftrightarrow x=2\left(N\right)\)
Với \(\left\{{}\begin{matrix}4a^2-5-2b=3\\4a^2-5+2b=7\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}4a^2-5+2b=7\\b=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}4a^4-10a^2+1=1\\b=1\end{matrix}\right.\)
\(\Leftrightarrow2a^2\left(2a^2-5\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}a^2=0\\2a^2=5\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-2\left(L\right)\\x=\dfrac{5}{2}-2\left(L\right)\end{matrix}\right.\)
Tương tự với hai trường hợp còn lại ta cũng ra nghiệm giống như trên.
Vậy \(x=2\) thì A là số chính phương
Tick nha bạn 😘
đề này ôn học sinh giỏi toán hả bạn?