Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(1,A=\left(\dfrac{\sqrt{x}}{\sqrt{x}-1}-\dfrac{1}{x-\sqrt{x}}\right):\left(\dfrac{1}{\sqrt{x}+1}+\dfrac{2}{x-1}\right)\left(x>0;x\ne1;x\right)\\ A=\dfrac{x-1}{\sqrt{x}\left(\sqrt{x}-1\right)}:\dfrac{\sqrt{x}-1+2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\\ A=\dfrac{\sqrt{x}+1}{\sqrt{x}}\cdot\left(\sqrt{x}-1\right)=\dfrac{x-1}{\sqrt{x}}\)
\(2,x=2\sqrt{2}+3=\left(\sqrt{2}+1\right)^2\\ \Leftrightarrow A=\dfrac{2\sqrt{2}+3}{\sqrt{2}+1}=\dfrac{\left(2\sqrt{2}+3\right)\left(\sqrt{2}-1\right)}{1}\\ =4\sqrt{2}-2\sqrt{2}+3\sqrt{2}-3=5\sqrt{2}-3\)


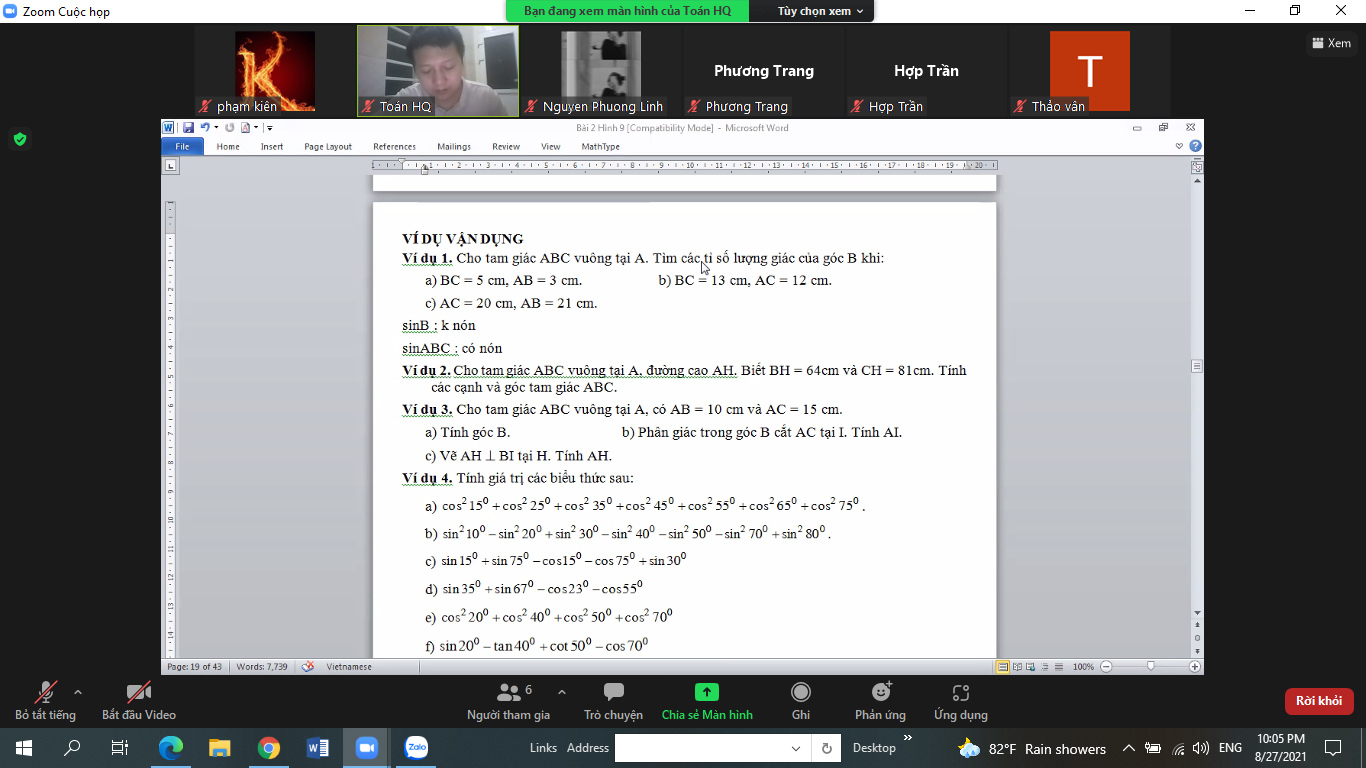
a: Áp dụng định lí Pytago vào ΔBAC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=10^2+15^2=325\)
hay \(BC=5\sqrt{13}\left(cm\right)\)
Xét ΔBAC vuông tại A có
\(\sin\widehat{B}=\dfrac{AC}{BC}=\dfrac{15}{5\sqrt{13}}=\dfrac{3}{\sqrt{13}}\)
\(\Leftrightarrow\widehat{B}\simeq56^0\)
b: Xét ΔBAC có
BI là đường phân giác ứng với cạnh AC
nên \(\dfrac{AI}{AB}=\dfrac{CI}{BC}\)
hay \(\dfrac{AI}{10}=\dfrac{CI}{5\sqrt{13}}\)
mà AI+CI=15cm
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{AI}{10}=\dfrac{CI}{5\sqrt{13}}=\dfrac{AI+CI}{10+5\sqrt{13}}=\dfrac{15}{10+5\sqrt{13}}=\dfrac{-2+\sqrt{13}}{3}\)
Do đó: \(AI=\dfrac{-20+10\sqrt{13}}{3}\left(cm\right)\)

a) Ta có: \(Q=\dfrac{3x+\sqrt{9x}-3}{x+\sqrt{x}-2}-\dfrac{\sqrt{x}+1}{\sqrt{x}+2}+\dfrac{\sqrt{x}-2}{1-\sqrt{x}}\)
\(=\dfrac{3x+3\sqrt{x}-3-\left(x-1\right)-\left(x-4\right)}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)}\)
\(=\dfrac{3x+3\sqrt{x}-3-x+1-x+4}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)}\)
\(=\dfrac{x+3\sqrt{x}+2}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)}\)
\(=\dfrac{\sqrt{x}+1}{\sqrt{x}-1}\)
b) Thay \(x=4+2\sqrt{3}\) vào Q, ta được:
\(Q=\dfrac{\sqrt{3}+1+1}{\sqrt{3}+1-1}=\dfrac{2+\sqrt{3}}{\sqrt{3}}=\dfrac{2\sqrt{3}+3}{3}\)
c) Để Q=3 thì \(\sqrt{x}+1=3\sqrt{x}-3\)
\(\Leftrightarrow\sqrt{x}-3\sqrt{x}=-3-1\)
\(\Leftrightarrow2\sqrt{x}=4\)
hay x=4
d) Để \(Q>\dfrac{1}{2}\) thì \(\dfrac{\sqrt{x}+1}{\sqrt{x}-1}-\dfrac{1}{2}>0\)
\(\Leftrightarrow\dfrac{2\sqrt{x}+2-\sqrt{x}+1}{2\left(\sqrt{x}-1\right)}>0\)
\(\Leftrightarrow\sqrt{x}-1>0\)
\(\Leftrightarrow x>1\)
Kết hợp ĐKXĐ, ta được: x>1
e) Để Q nguyên thì \(\sqrt{x}+1⋮\sqrt{x}-1\)
\(\Leftrightarrow2⋮\sqrt{x}-1\)
\(\Leftrightarrow\sqrt{x}-1\in\left\{-1;1;2\right\}\)
\(\Leftrightarrow\sqrt{x}\in\left\{0;2;3\right\}\)
hay \(x\in\left\{0;4;9\right\}\)


a: Xét (O) có
CM là tiếp tuyến có M là tiếp điểm
CN là tiếp tuyến có N là tiếp điểm
Do đó: CM=CN
hay C nằm trên đường trung trực của MN(1)
Ta có: OM=ON
nên O nằm trên đường trung trực của MN(2)
Từ (1) và (2) suy ra OC là đường trung trực của MN

Bài I:
1: Thay x=4 vào A, ta được:
\(A=\dfrac{4}{2+1}=\dfrac{4}{3}\)
2: \(B=\dfrac{3}{\sqrt{x}+1}+\dfrac{x+5}{x-1}-\dfrac{1}{\sqrt{x}-1}\)
\(=\dfrac{3}{\sqrt{x}+1}+\dfrac{\left(x+5\right)}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}-\dfrac{1}{\sqrt{x}-1}\)
\(=\dfrac{3\left(\sqrt{x}-1\right)+x+5-\sqrt{x}-1}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}\)
\(=\dfrac{3\sqrt{x}-3+x-\sqrt{x}+4}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}=\dfrac{x+2\sqrt{x}+1}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}\)
\(=\dfrac{\left(\sqrt{x}+1\right)^2}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}=\dfrac{\sqrt{x}+1}{\sqrt{x}-1}\)
3: P=A*B
\(=\dfrac{\sqrt{x}+1}{\sqrt{x}-1}\cdot\dfrac{x}{\sqrt{x}+1}=\dfrac{x}{\sqrt{x}-1}\)
P<=4
=>P-4<=0
=>\(\dfrac{x-4\sqrt{x}+4}{\sqrt{x}-1}< =0\)
=>\(\dfrac{\left(\sqrt{x}-2\right)^2}{\sqrt{x}-1}< =0\)
=>\(\sqrt{x}-1< 0\)
=>\(\sqrt{x}< 1\)
=>0<=x<1
Kết hợp ĐKXĐ, ta được: 0<=x<1
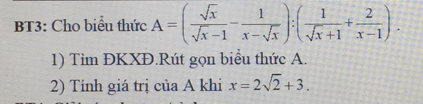
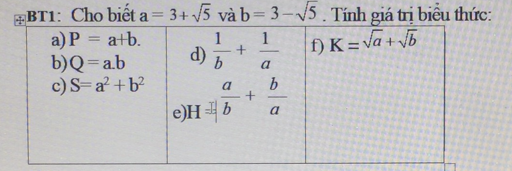

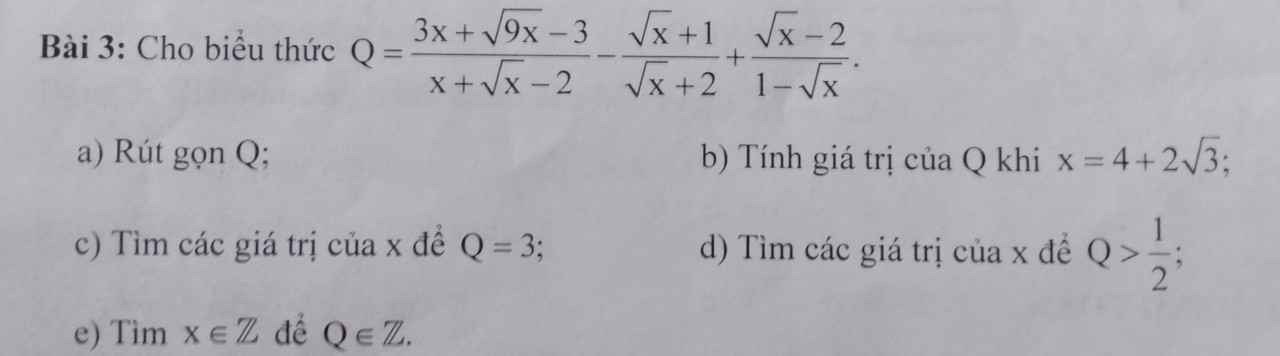 giúp mình vs mình đg cần gấp
giúp mình vs mình đg cần gấp