
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


10:
a: (SB;(ABC))=(BS;BA)=góc BSA
tan BSA=AB/SA=1/căn 3
=>góc BSA=30 độ
b: BC vuông góc AB
BC vuông góc SA
=>BC vuông góc (SAB)
=>BC vuông góc AH
mà AH vuông góc SB
nên AH vuông góc (SBC)
=>AH vuông góc SC
mà HK vuông góc SC
nên SC vuông góc (AHK)



6.
Do \(AA'\perp\left(ABCD\right)\) (t/c hình hộp chữ nhật)
Mà \(AA'\in\left(ACC'A'\right)\)
\(\Rightarrow\left(ACC'A'\right)\perp\left(ABCD\right)\Rightarrow\) góc giữa (ACC'A') avf (ABCD) bằng 90 độ
b.
Từ H kẻ AH vuông góc BD (H thuộc BD)
Do \(AA'\perp\left(ABCD\right)\Rightarrow AA'\perp BD\)
\(\Rightarrow BD\perp\left(A'AH\right)\)
\(\Rightarrow\left\{{}\begin{matrix}BD\perp AH\\BD\perp A'H\end{matrix}\right.\)
Mà \(BD=\left(A'BD\right)\cap\left(ABCD\right)\Rightarrow\widehat{AHA'}\) là góc giữa (A'BD) và (ABCD)
\(AH=\dfrac{AB.AD}{\sqrt{AB^2+AD^2}}=\dfrac{bc}{\sqrt{b^2+c^2}}\)
\(\Rightarrow tan\widehat{AHA'}=\dfrac{AA'}{AH}=\dfrac{a\sqrt{b^2+c^2}}{bc}\)
7.
Kẻ \(AI\perp CM\Rightarrow\widehat{IAM}=\widehat{BCM}\) (góc có cạnh tương ứng vuông góc)
\(CM=\sqrt{BC^2+BM^2}=\sqrt{BC^2+\left(\dfrac{AB}{2}\right)^2}=2a\)
\(\Rightarrow AI=AM.cos\widehat{IAM}=\dfrac{AB}{2}.cos\widehat{BCM}=\dfrac{AB}{2}.\dfrac{BC}{CM}=\dfrac{a\sqrt{3}}{2}\)
b.
\(\left\{{}\begin{matrix}SA\perp\left(ABC\right)\Rightarrow SA\perp CI\\CI\perp AI\left(gt\right)\end{matrix}\right.\) \(\Rightarrow CI\perp\left(SAI\right)\Rightarrow\left\{{}\begin{matrix}CI\perp SI\\CI\perp AI\end{matrix}\right.\)
Mà \(CI=\left(SMC\right)\cap\left(ABC\right)\Rightarrow\widehat{SIA}\) là góc giữa (SMC) và (ABC)
\(tan\widehat{SIA}=\dfrac{SA}{AI}=\dfrac{4\sqrt{3}}{3}\Rightarrow\widehat{SIA}\approx66^035'\)


c)\(\left\{{}\begin{matrix}u_1+u_3=3\\u_1^2+u_3^2=5\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}u_1+u_3=3\\\left(u_1+u_3\right)^2-2u_1u_3=5\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}u_1+u_3=3\\u_1u_3=2\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}u_1=2\\u_3=1\end{matrix}\right.\\\left\{{}\begin{matrix}u_1=1\\u_3=2\end{matrix}\right.\end{matrix}\right.\)
Làm nốt (sử dụng công thức: \(u_n=u_1+\left(n-1\right)d\) để tìm được công sai
\(S_n=nu_1+\dfrac{n\left(n-1\right)}{2}d\) để tính tổng 15 số hạng đầu)
d)\(\left\{{}\begin{matrix}u_1+u_2+u_3=14\\u_1u_2u_3=64\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}u_2-d+u_2+u_2+d=14\\\left(u_2-d\right)u_2\left(u_2+d\right)=64\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}u_2=\dfrac{14}{3}\\\left(u_2^2-d^2\right)u_2=64\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}\dfrac{14}{3}=u_2=u_1+d\\d=\dfrac{2\sqrt{889}}{21}\end{matrix}\right.\\\left\{{}\begin{matrix}\dfrac{14}{3}=u_1+d\\d=\dfrac{-2\sqrt{889}}{21}\end{matrix}\right.\end{matrix}\right.\)
(Làm nốt,số xấu quá)
e)\(\left\{{}\begin{matrix}u_1+u_2+u_3=7\\u_1^2+u_2^2+u_3^2=21\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}u_1+u_2+u_3=7\\u_1u_2u_3=\dfrac{21-\left(u_1+u_2+u_3\right)^2}{2}=-14\end{matrix}\right.\)
Làm như ý d)
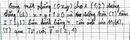




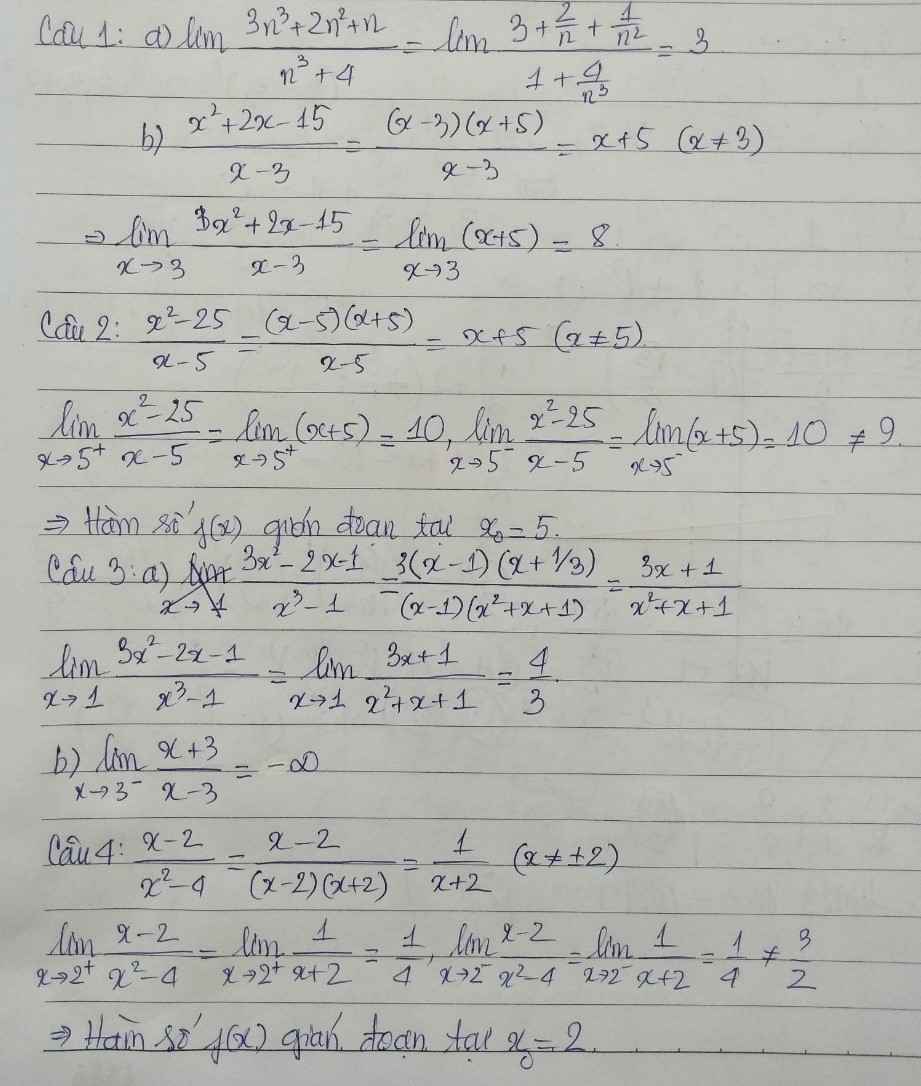
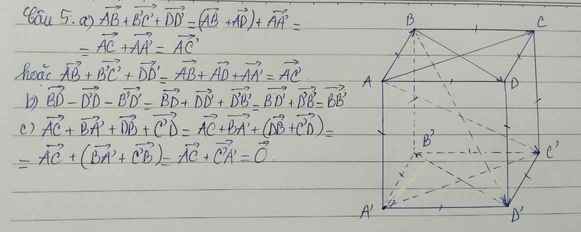








- \(T_{\overrightarrow{v}}\left(A\right)=A'\left(3,3\right)\)
- \(y=-x-1\)qua phép tịnh tiến thì được điểm song song hoặc trùng với nó nên đường thẳng \(d'\)(là ảnh của \(d\)) có dạng \(y=-x+a\). Chọn \(B\left(-1,0\right)\in\left(d\right)\Rightarrow T_{\overrightarrow{v}}\left(B\right)=B'\left(1,1\right)\in\left(d'\right)\)
Có: \(1=-1+a\Leftrightarrow a=2\Rightarrow\left(d'\right):y=-x+2\)
- \(T_{\overrightarrow{v}}\left(I\right)=I'\left(4,4\right)\)suy ra ảnh \(\left(T'\right)\)của \(\left(T\right)\): \(\left(x-4\right)^2+\left(y-4\right)^2=4^2\)