
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\left(d\right):\frac{x}{a}+\frac{y}{b}=1\)\(\left(1\right)\)
Thế \(x=a,y=0\)vào phương trình \(\left(1\right)\)thỏa mãn nên \(A\left(a,0\right)\)thuộc \(\left(d\right)\).
Thế \(x=0,y=b\)vào phương trình \(\left(1\right)\)thỏa mãn nên \(B\left(0,b\right)\)thuộc \(\left(d\right)\).
Do đó ta có đpcm.


\(\sqrt{a^2+3}=\sqrt{a^2+ab+bc+ca}=\sqrt{\left(a+b\right)\left(a+c\right)}\le\dfrac{1}{2}\left(a+b+a+c\right)=\dfrac{1}{2}\left(2a+b+c\right)\)
Tương tự: \(\sqrt{b^2+3}\le\dfrac{1}{2}\left(a+2b+c\right)\) ; \(\sqrt{c^2+3}\le\dfrac{1}{2}\left(a+b+2c\right)\)
Cộng vế với vế:
\(VT\le\dfrac{1}{2}\left(4a+4b+4c\right)=2\left(a+b+c\right)\)

\(=\dfrac{\sqrt{x}\left(\sqrt{x}-1\right)}{\sqrt{x}-1}+\dfrac{\sqrt{x}\left(\sqrt{x}+1\right)}{\sqrt{x}+1}\)
\(=\sqrt{x}+\sqrt{x}=2\sqrt{x}\)

1.theo bất đẳng thức côsi ta có
\(a+b\ge2\sqrt{ab}\\ b+c\ge2\sqrt{ab}\\ c+a\ge2\sqrt{ab}\)
\(\Rightarrow\left(a+b\right)\left(b+c\right)\left(c+a\right)\ge8\sqrt{ab.bc.ca}\)
\(\ge8\sqrt{a^2b^2c^2}\\ \ge8abc\)
2.\(a^4+b^2\ge2\sqrt{a^4b^2}=2a^4b^2\)
\(\dfrac{a}{a^4+b^2}\le\dfrac{a}{2a^2b}=\dfrac{1}{2ab}\)
tương tự:\(\dfrac{b}{b^4+a^2}\le\dfrac{1}{2ab}\)
\(\rightarrow\dfrac{a}{a^4+b^2}+\dfrac{b}{b^4+a^2}\le\dfrac{1}{ab}\)
dấu = xảy ra khi \(a^4=b^2\\ b^4=a^2\)\(\rightarrow a^2=b^2=1\)

Lần sau đăng tách bài ra bạn nhé.
Câu 8

Câu 1, ý a và b:
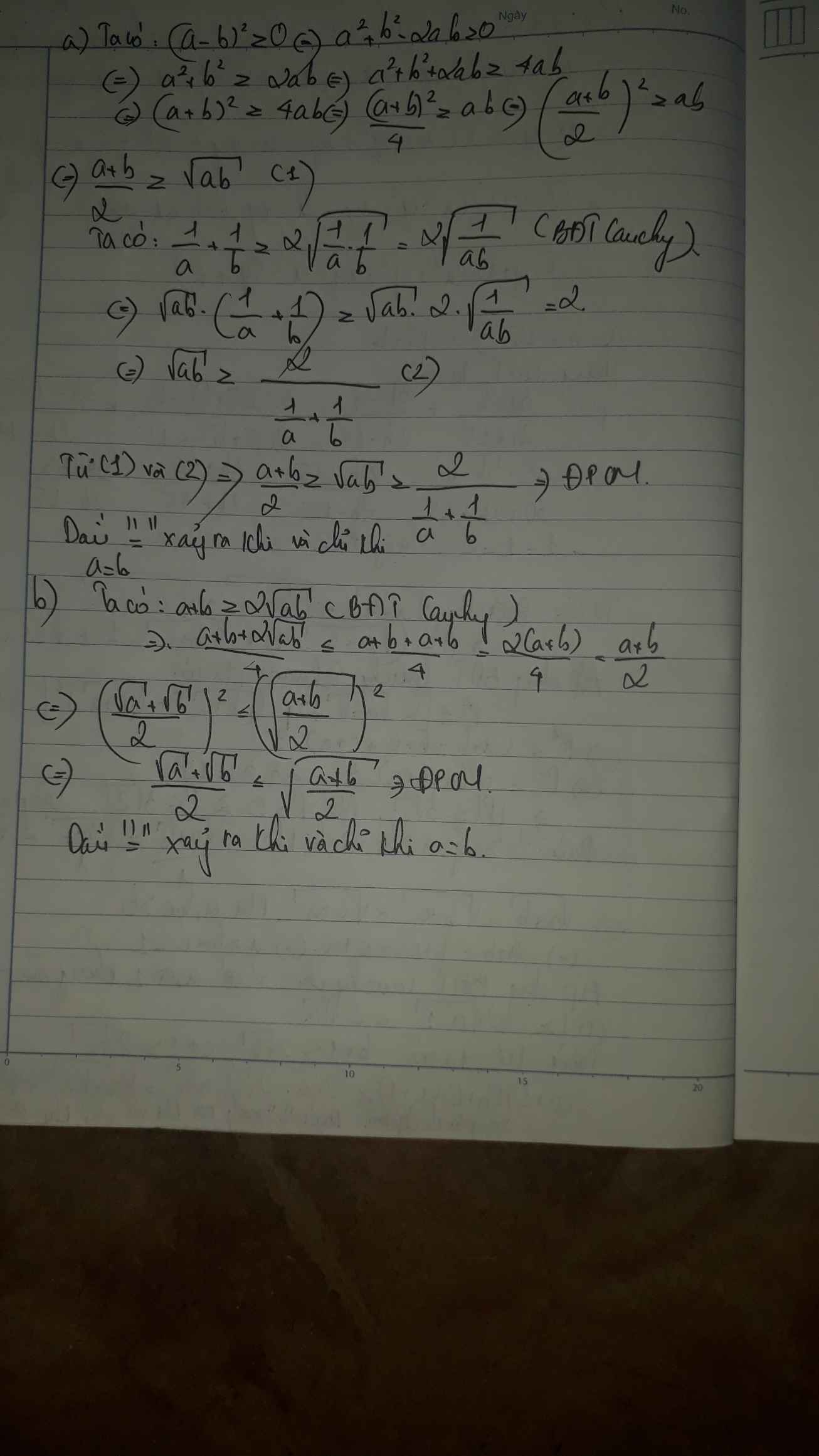
Câu 7:
Ta có: \(\dfrac{x}{\sqrt{4x-1}}\ge\dfrac{1}{2}\)
\(\Leftrightarrow\dfrac{2x-\sqrt{4x-1}}{2\sqrt{4x-1}}\ge0\)
\(\Leftrightarrow2x-\sqrt{4x-1}\ge0\)
\(\Leftrightarrow4x-2\sqrt{4x-1}\ge0\)
\(\Leftrightarrow4x-1-2\cdot\sqrt{4x-1}\cdot1+1\ge0\)
\(\Leftrightarrow\left(\sqrt{4x-1}-1\right)^2\ge0\forall x\) thỏa mãn ĐKXĐ

2: Thay x=1 và y=-4 vào (d), ta được:
2m+2=-4
hay m=-3

Ai giỏi toán giúp mình câu này với
giải phương trình: \(\left(2x^2-6x+5\right)\left(2x-3\right)^2=1\)

\(\left(2x^2-6x+5\right)\left(2x-3\right)^2=1\)
\(\Leftrightarrow\left[2\left(2x^2-6x+5\right)\right].\left(2x-3\right)^2=2.1\)
\(\Leftrightarrow\left(4x^2-12x+10\right)\left(2x-3\right)^2=2\)
\(\Leftrightarrow\left[\left(2x\right)^2-2.2x.3+3^2+1\right]\left(2x-3\right)^2=2\)
\(\Leftrightarrow\left[\left(2x-3\right)^2+1\right]\left(2x-3\right)^2=2\) (1)
Đặt \(\left(2x-3\right)^2=c\left(c\ge0\right)\)
Suy ra (1) trở thành: \(c\left(c+1\right)=2\)
\(\Leftrightarrow\left(c-1\right)\left(c+2\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}c-1=0\\c+2=0\end{cases}\Leftrightarrow\orbr{\begin{cases}c=1\\c=-2\end{cases}}}\)
Vì \(c\ge1\) nên c = 1
Hay \(\Rightarrow\left(2x-3\right)^2=1\)
\(\Rightarrow\orbr{\begin{cases}2x-3=1\\2x-3=-1\end{cases}\Leftrightarrow\orbr{\begin{cases}x=2\\x=1\end{cases}}}\)
Vậy phương trình có hai nghiệm là x = 1 hoặc x = 2
P/s: Bài giải có nhiều sai sót, chị xem lại giúp em.
P/s: Chữ (h) nghĩa là "hoặc"
\(\left(2x^2-6x+5\right)\left(2x-3\right)^2=1\)
Do 1 là số dương nên \(\left(2x^2-6x+5\right)\) và \(\left(2x-3\right)^2\) đồng dấu.
Mà \(\left(2x-3\right)^2\ge0\forall x\) nên chỉ cần xét 1 trường hợp:
\(\hept{\begin{cases}2x^2-6x+5=1\\\left(2x-3\right)^2=1\end{cases}}\Leftrightarrow\hept{\begin{cases}2x^2-6x+4=0\\2x-3=1..\left(h\right)..2x-3=-1\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}2\left(x-2\right)\left(x-1\right)=0\\2x=4...\left(h\right)...2x=2\end{cases}}\Leftrightarrow x=2...\left(h\right)...x=1\)
Vậy x = 2 hoặc x = 1
 ai giúp mình giải câu này với ạ, mình cám ơn mn nhiều
ai giúp mình giải câu này với ạ, mình cám ơn mn nhiều
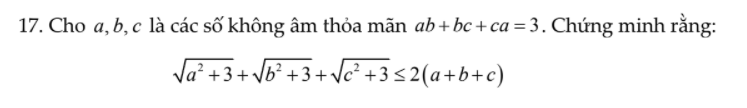 câu này với ạ! Mình cảm ơn.
câu này với ạ! Mình cảm ơn.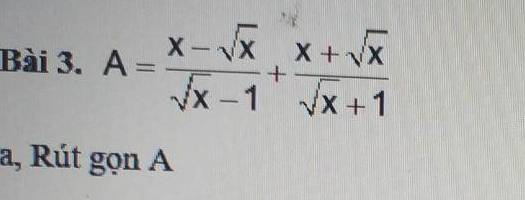
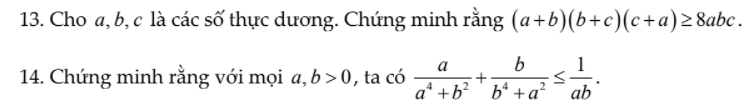




Ta có
\(\widehat{ACH}=180^o-\left(\widehat{AHC}+\widehat{HAC}\right)=180^o-\left(90^o+30^o\right)=60^o\)
\(\Rightarrow\cos\widehat{ACH}=\frac{CH}{AC}\Rightarrow\cos60^o=\frac{20}{AC}\Rightarrow AC=\frac{20}{\cos60^o}=40m\)
Xét tg vuông AHC có
\(AH=\sqrt{AC^2-CH^2}=20\sqrt{3}m\)
Xét tg vuông BHC có
\(\widehat{HCB}=45^o\Rightarrow\widehat{HBC}=45^o\Rightarrow\widehat{HCB}=\widehat{HBC}\Rightarrow\Delta HBC\) cân tại H => HC=HB=20 m
\(\Rightarrow AB=AH-HB=20\sqrt{3}-20=20\left(\sqrt{3}-1\right)m\)