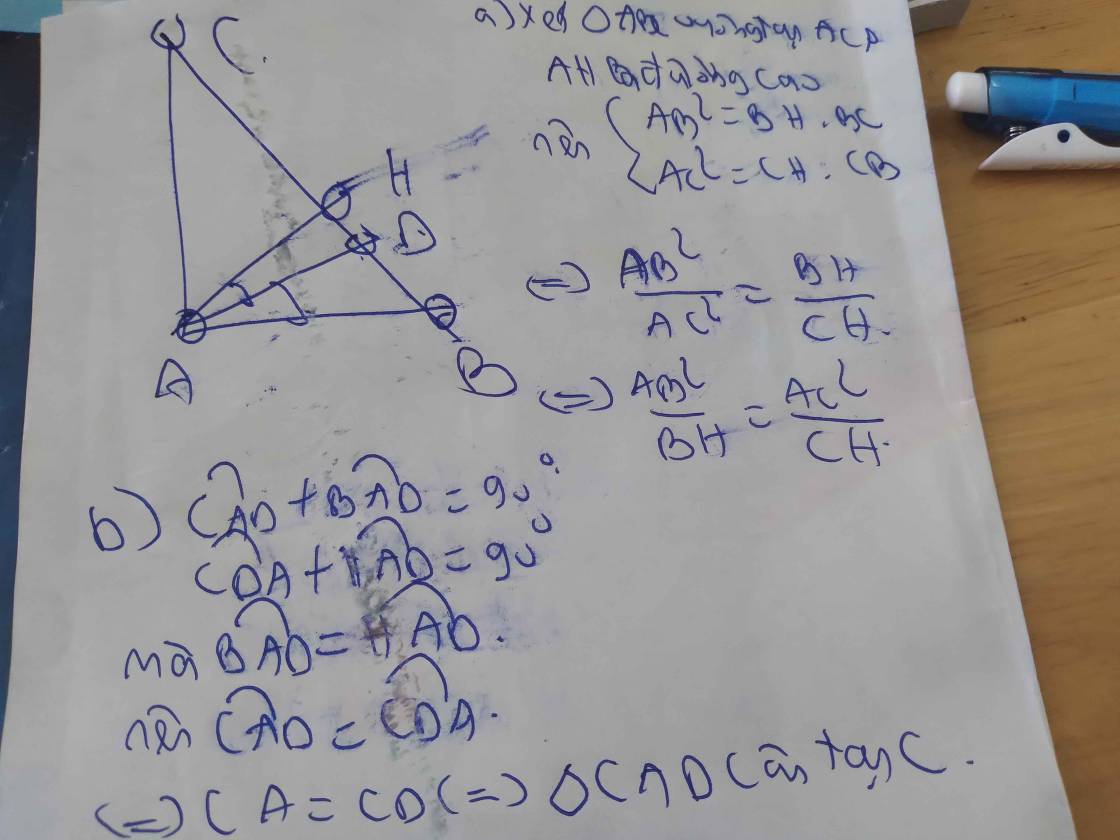Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Để đồ thị hàm số \(y=\left(2m+2\right)x-5m\)song song với đường thẳng \(y=4x+1\)thì:
\(\hept{\begin{cases}2m+2=4\\-5m\ne1\end{cases}}\Leftrightarrow m=1\).

Để hs trên bậc nhất khi \(a\ne0\)
Thay x = 3 ; y = 4 vào đths trên ta được : \(4=3a+8\Leftrightarrow a=-\frac{4}{3}\)( tm )

Ta có: mx-y=6 <=> (d):y=mx-6
3x+my=3 <=> (d'): y= \(\frac{3-3x}{m}\)(m \(\ne\)0)
Xét pt hoành độ giao điểm của (d) và (d'), ta được:
mx-6=\(\frac{3-3x}{m}\)
\(\Leftrightarrow\)\(m^2x-6m=3-3x\)
\(\Leftrightarrow x=\frac{6m+3}{m^2+3}\)
Do đó, y=\(mx-6=\frac{6m+3}{m^2+3}\times m-6=\frac{3m-18}{m^2+3}\)
Khi đó, M\(\left(\frac{6m+3}{m^2+3}+\frac{3m-18}{m^2+3}\right)\)là giao điểm của (d) và (d')
Để M thuộc góc phần tư thứ IV thì
\(\hept{\begin{cases}\frac{6m+3}{m^2+3}>0\\\frac{3m-18}{m^2+3}< 0\end{cases}}\)\(\Leftrightarrow\hept{\begin{cases}6m+3>0\\3m-18< 0\end{cases}}\)(Vì \(m^2\)+3>0, với mọi m)\(\Leftrightarrow\hept{\begin{cases}m>\frac{-1}{2}\\m< 6\end{cases}\Leftrightarrow\frac{-1}{2}< m< 6}\)
Vậy.......

P(x) = 0
=> (4m + 5x - 2)x + (6m - 7n - 6) = 0 \(\forall x\)
=> \(\hept{\begin{cases}4m+5n-2=0\\6m-7n-6=0\end{cases}}\Rightarrow\hept{\begin{cases}4m+5n=2\\6m-7n=6\end{cases}}\Rightarrow\hept{\begin{cases}n=\frac{-6}{29}\\m=\frac{22}{29}\end{cases}}\)
Vậy m = -6/29; n = 22/29 thì P(x) = 0


ta có :
\(\hept{\begin{cases}AB^2=BD.BC=9\left(9+16\right)=225\\AC^2=CD.CB=16\left(16+9\right)=400\end{cases}}\Leftrightarrow\hept{\begin{cases}AB=15\\AC=20\end{cases}}\)
nên diện tích ABC là : \(\frac{1}{2}AB.AC=\frac{1}{2}.15.20=150cm^2\)

| 1 | 3 | h | d | K | y | b | a | k | kkkkqq | k | k | k | k | k | k8 | 7 | 5 | 4 | 0 | 6 | 3 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 9 | 8 | 7 | 6 | 4 | 9 | 6 | 9 | 6 | 8 | 9 | 7 | 8 | 99 | 7 | 5 | 8 | 90 | 8 | 9 | 7 | ||
| 67 | 89 | 9 | 7 | 8 | 8 | 97 | 989 | 789 | 90 | 8 | 9 | 00 | 8 | 9 | 8 | 9 | 09 | 78 | 9 | 8 | 8 |
\(\left(d_2\right):2x-y=-2\) \(\left(d_3\right)2x-2y=-4\)
\(\Leftrightarrow\left(d_2\right):y=2x+2\) \(\left(d_3\right):y=x+2\)
Hoành độ của giao điểm là No của
\(2x+2=x+2\)
\(\Leftrightarrow x=0\)
Thay vào pt d3 , ta có:
\(y=0+2=2\)
Vậy giao điểm của d2 và d3 là tại
A(0;2)
Để 3 đường đồng quy thì, thay A(0;2) hay x=0 ;y= 2 vào d
\(4.m.0+\left(3m-5\right).2=5m+4\)
\(\Leftrightarrow6m-10=5m+4\)
\(\Leftrightarrow m=14\)
Vậy để 3 đường thẳng trên đồng quy thì = 14