
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(a,x+\dfrac{1}{2}=\dfrac{3}{4}\\ x=\dfrac{3}{4}-\dfrac{1}{2}\\ x=\dfrac{1}{2}\\ b,-\dfrac{2}{3}-x=1\\x=-\dfrac{2}{3}-1\\ x=-\dfrac{5}{3}\\ d,\dfrac{1}{4}+\dfrac{3}{4}:x=\dfrac{5}{2}\\ \dfrac{3}{4}:x=\dfrac{5}{2}-\dfrac{1}{4}\\ \dfrac{3}{4}:x=\dfrac{9}{4}\\ x=\dfrac{3}{4}:\dfrac{9}{4}\\ x=\dfrac{1}{3}\\ e,\left(x+\dfrac{1}{4}\right)\cdot\dfrac{3}{4}=-\dfrac{5}{8}\\ x+\dfrac{1}{4}=-\dfrac{5}{8}:\dfrac{3}{4}\\ x+\dfrac{1}{4}=\dfrac{5}{6}\\ x=\dfrac{5}{6}-\dfrac{1}{4}\\ x=\dfrac{7}{12}\)
\(g,\dfrac{x-3}{15}=\dfrac{-2}{5}\\ 5\left(x-3\right)=-30\\ x-3=-6\\ x=-6+3\\ x=-3\\ h,\dfrac{x}{-2}=\dfrac{-8}{x}\\ x^2=16\\ x=\pm\sqrt{16}\\ x=\pm4\\ k,\dfrac{x+2}{3}=\dfrac{x-4}{5}\\ 5\left(x+2\right)=3\left(x-4\right)\\ 5x+10=3x-12\\ 5x-3x=-12-10\\ 2x=-22\\ x=-11\)
\(m,\left(2x-1\right)^2=4\\ \Rightarrow\left[{}\begin{matrix}2x-1=2\\2x-1=-2\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}2x=3\\2x=-1\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=\dfrac{3}{2}\\x=-\dfrac{1}{2}\end{matrix}\right.\)

a: Xét ΔBAD vuông tại A và ΔBED vuông tại E có
BD chung
\(\widehat{ABD}=\widehat{EBD}\)
Do đó: ΔBAD=ΔBED



Bài 1:
a, \(\dfrac{2}{3}\) + \(\dfrac{1}{5}\). \(\dfrac{10}{7}\)
= \(\dfrac{2}{3}\) + \(\dfrac{2}{7}\)
= \(\dfrac{20}{21}\)
b, \(\dfrac{7}{12}\) - \(\dfrac{27}{7}\). \(\dfrac{1}{18}\)
= \(\dfrac{7}{12}\) - \(\dfrac{3}{14}\)
= \(\dfrac{31}{84}\)
c, \(\dfrac{3}{10}\). \(\dfrac{-5}{6}\) - \(\dfrac{1}{8}\)
= - \(\dfrac{1}{4}\) - \(\dfrac{1}{8}\)
= - \(\dfrac{3}{8}\)
d, - \(\dfrac{4}{9}\): \(\dfrac{8}{3}\) + \(\dfrac{1}{18}\)
= - \(\dfrac{1}{6}\) + \(\dfrac{1}{18}\)
= - \(\dfrac{1}{9}\)
e, {[(\(\dfrac{1}{2}\) - \(\dfrac{2}{3}\))2 : 2 ] - 1}. \(\dfrac{4}{5}\)
= {[ (-\(\dfrac{1}{6}\))2 : 2] - 1}. \(\dfrac{4}{5}\)
= { [\(\dfrac{1}{36}\) : 2] - 1}. \(\dfrac{4}{5}\)
= { \(\dfrac{1}{72}\) - 1}. \(\dfrac{4}{5}\)
=- \(\dfrac{71}{72}\).\(\dfrac{4}{5}\)
= -\(\dfrac{71}{90}\)

Bài 77:
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{8}=\dfrac{y}{9}=\dfrac{y-x}{9-8}=5\)
Do đó: x=40; y=45

6:
\(2^{225}=\left(2^3\right)^{75}=8^{75}\)
\(3^{150}=\left(3^2\right)^{75}=9^{75}\)
mà 8<9
nên \(2^{225}< 3^{150}\)
4: \(\left|5x+3\right|>=0\forall x\)
=>\(-\left|5x+3\right|< =0\forall x\)
=>\(-\left|5x+3\right|+5< =5\forall x\)
Dấu = xảy ra khi 5x+3=0
=>x=-3/5
1:
\(\left(2x+1\right)^4>=0\)
=>\(\left(2x+1\right)^4+2>=2\)
=>\(M=\dfrac{3}{\left(2x+1\right)^4+2}< =\dfrac{3}{2}\)
Dấu = xảy ra khi 2x+1=0
=>x=-1/2

1: \(\sqrt{11}\) là số vô tỉ
2:
a: 4,9(18)=4,91818...
mà 4,91818<4,928
nên 4,9(18)<4,928
b: 4,315<4,318
=>-4,315>-4,318
=>-4,315...>-4,318...
c: \(\sqrt{3}=\sqrt{\dfrac{6}{2}}< \sqrt{\dfrac{7}{2}}\)
3:
a: \(6=\sqrt{3};-1,7=-\sqrt{2,89}\)
0<2,89<3
=>\(0< \sqrt{2,89}< \sqrt{3}\)
=>\(-\sqrt{3}< -\sqrt{2,89}< 0\)
0<35<36<47
=>\(0< \sqrt{35}< \sqrt{36}< \sqrt{47}\)
=>\(-\sqrt{3}< -\sqrt{2,89}< 0< \sqrt{35}< \sqrt{36}< \sqrt{47}\)
=>\(-\sqrt{3}< -\sqrt{2,89}< 0< \sqrt{35}< 6< \sqrt{47}\)
b: \(-\sqrt{2\dfrac{1}{3}}=-\sqrt{2,\left(3\right)}\)
\(-1,5=-\sqrt{2,25}\)
2,25<2,3<2,(3)
=>\(\sqrt{2.25}< \sqrt{2.3}< \sqrt{2.\left(3\right)}\)
=>\(0>-1.5>-\sqrt{2.3}>-\sqrt{2\dfrac{1}{3}}\)
\(0< \sqrt{5\dfrac{1}{6}}=\sqrt{5,1\left(6\right)}< \sqrt{5,3}\)
=>\(\sqrt{5.3}>\sqrt{5\dfrac{1}{6}}>0>-1.5>-\sqrt{2.3}>-\sqrt{2\dfrac{1}{3}}\)
 giúp em với ạ ai làm đc thì em xin cảm ơn ạ em đang cần gấp được ko ạ
giúp em với ạ ai làm đc thì em xin cảm ơn ạ em đang cần gấp được ko ạ

 giúp em 3 bài này với ạ em đang cần gấp chiều em hc ròi ạ ai làm đc bài nào thì gửi luôn giúp em ạ
giúp em 3 bài này với ạ em đang cần gấp chiều em hc ròi ạ ai làm đc bài nào thì gửi luôn giúp em ạ

 ai giải giúp em từ 3 đến bài 12 với ạ em đang cần gấp chiều em đi thi ạ
ai giải giúp em từ 3 đến bài 12 với ạ em đang cần gấp chiều em đi thi ạ
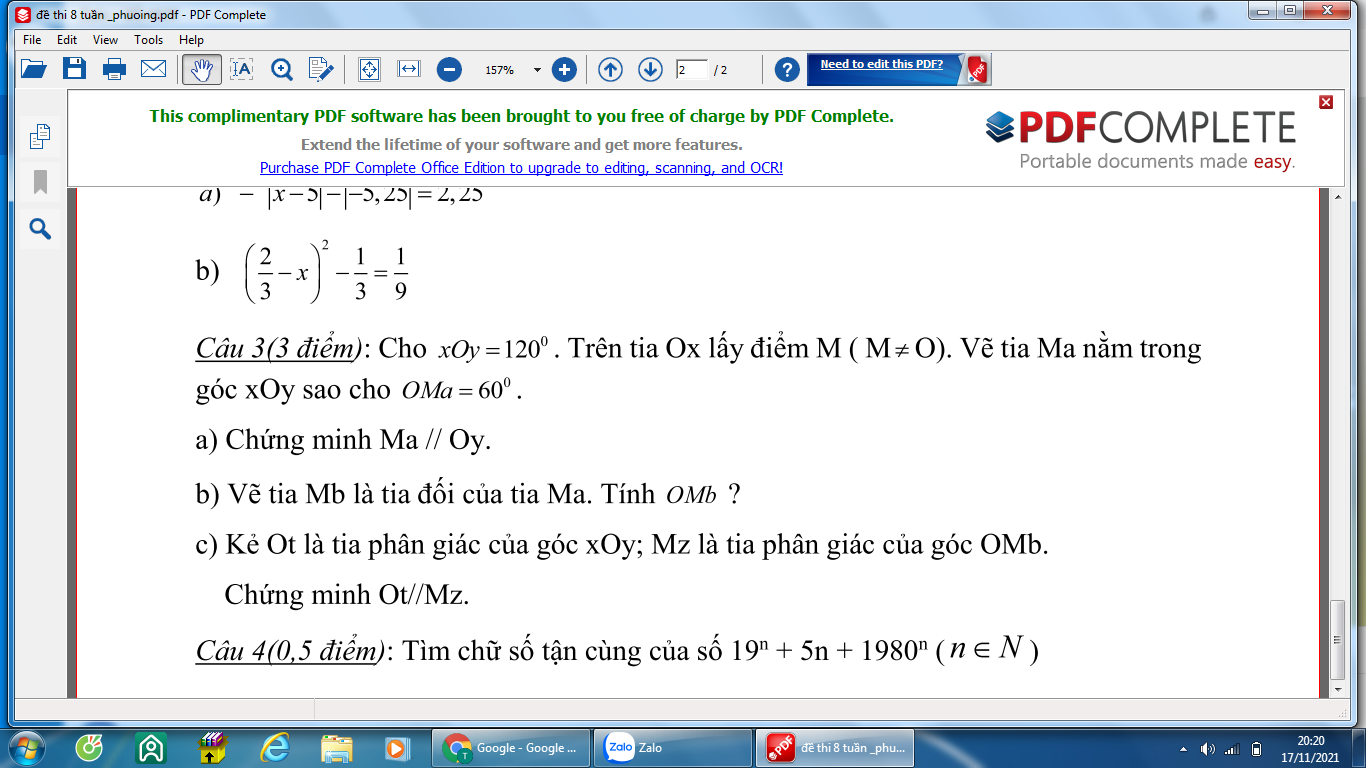

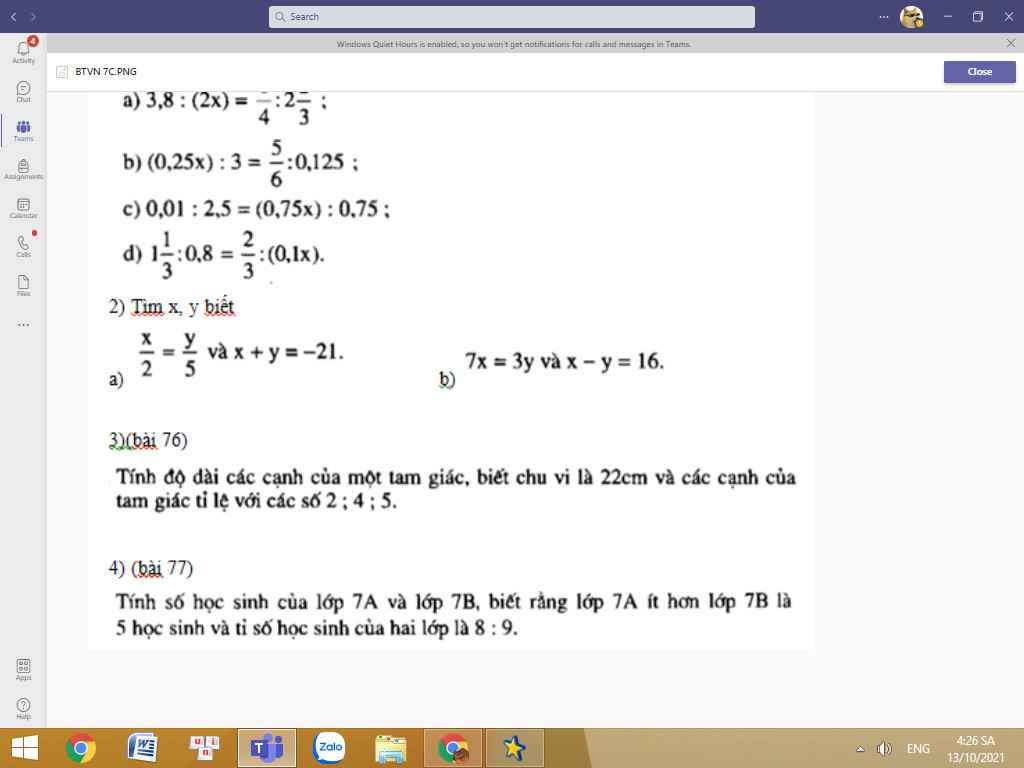 ai giúp em làm câu này vs em đang cần gấp ạ
ai giúp em làm câu này vs em đang cần gấp ạ giúp em với ạ em đang cần gấp ạ. Bài nào làm đc trc thì làm trc giúp em với ạ
giúp em với ạ em đang cần gấp ạ. Bài nào làm đc trc thì làm trc giúp em với ạ giúp em với ạ em cần gấp ạ
giúp em với ạ em cần gấp ạ
bài nào v
có gì đâumà giúp