
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 2:
Ta có: \(3n^3+10n^2-5⋮3n+1\)
\(\Leftrightarrow3n^3+n^2+9n^2+3n-3n-1-4⋮3n+1\)
\(\Leftrightarrow3n+1\in\left\{1;-1;2;-2;4;-4\right\}\)
\(\Leftrightarrow3n\in\left\{0;-3;3\right\}\)
hay \(n\in\left\{0;-1;1\right\}\)

CẤM KÉO CẦU THANG XUỐNG
╬═╬
╬═╬
╬═╬
╬═╬
╬═╬
╬═╬
╬═╬
╬═╬
╬═╬
╬═╬
╬═╬
╬═╬
╬═╬
╬═╬
╬═╬
╬═╬TUI-NÓI-CẤM
╬═╬
╬═╬
╬═╬
╬═╬
╬═╬
╬═╬
╬═╬
╬═╬
╬═╬Dừng lại! Đừng đi xuống.
╬═╬
╬═╬
╬═╬
╬═╬
╬═╬
╬═╬
╬═╬
╬═╬
╬═╬ Bạn nghe tui! Đừng đi xuống đó
╬═╬
╬═╬
╬═╬
╬═╬
╬═╬
╬═╬
╬═╬
╬═╬Bạn thật là đần độn khi cứ phớt lờ câu nói của tui như vậy đó....
╬═╬
╬═╬
╬═╬
╬═╬Nghiêm túc!!!TUI NÓI DỪNG LẠI!
╬═╬Cơ hội cuối cùng...đừng xuống đó
╬═╬
╬═╬
bây giờ bạn sẽ có 5 năm không may mắn, trừ khi bạn đăng câu này trên 5 web khác nhau~~
Đã bảo rồi mà ko nghe người ta cơ 🙂CẤM KÉO CẦU THANG XUỐNG
╬═╬
╬═╬
╬═╬
╬═╬
╬═╬
╬═╬
╬═╬
╬═╬
╬═╬
╬═╬
╬═╬
╬═╬
╬═╬
╬═╬
╬═╬
╬═╬TUI-NÓI-CẤM
╬═╬
╬═╬
╬═╬
╬═╬
╬═╬
╬═╬
╬═╬
╬═╬
╬═╬Dừng lại! Đừng đi xuống.
╬═╬
╬═╬
╬═╬
╬═╬
╬═╬
╬═╬
╬═╬
╬═╬
╬═╬ Bạn nghe tui! Đừng đi xuống đó
╬═╬
╬═╬
╬═╬
╬═╬
╬═╬
╬═╬
╬═╬
╬═╬Bạn thật là đần độn khi cứ phớt lờ câu nói của tui như vậy đó....
╬═╬
╬═╬
╬═╬
╬═╬Nghiêm túc!!!TUI NÓI DỪNG LẠI!
╬═╬Cơ hội cuối cùng...đừng xuống đó
╬═╬
╬═╬
bây giờ bạn sẽ có 5 năm không may mắn, trừ khi bạn đăng câu này trên 5 web khác nhau~~
Đã bảo rồi mà ko nghe người ta cơ 🙂



\(\left(x-4\right)^2=\left(2x+1\right)^2\)
\(\Leftrightarrow\left(x-4\right)^2-\left(2x+1\right)^2=0\)
\(\Leftrightarrow\left(x-4-2x-1\right)\left(x-4+2x+1\right)=0\)
\(\Leftrightarrow\left(x-5\right)\left(3x-3\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x-5=0\\3x-3=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=5\\3\left(x-1\right)=0\end{cases}}}\)
\(\Leftrightarrow\orbr{\begin{cases}x=5\\x-1=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=5\\x=1\end{cases}}}\)

a.
Ta có \(BD||AC\) (cùng vuông góc AB)
Áp dụng định lý Talet trong tam giác ACE: \(\dfrac{BE}{BA}=\dfrac{DE}{DC}\)
b.
Ta có \(IK||BD||AC\) \(\Rightarrow EI||AC\)
Áp dụng Talet: \(\dfrac{DC}{ED}=\dfrac{DA}{ID}\Rightarrow\dfrac{DC}{DC+ED}=\dfrac{DA}{DA+ID}\Rightarrow\dfrac{DC}{CE}=\dfrac{DA}{AI}\) (1)
Do \(BD||EK\), áp dụng Talet trong tam giác CEK: \(\dfrac{BD}{EK}=\dfrac{CD}{CE}\) (2)
Do \(BD||EI\), áp dụng Talet trong tam giác AEI: \(\dfrac{BD}{EI}=\dfrac{AD}{AI}\) (3)
Từ(1);(2);(3) \(\Rightarrow\dfrac{BD}{EK}=\dfrac{BD}{EI}\Rightarrow EK=EI\)

`3)(x+4)/(x-3)-(x-3)/(x+4)=(x^2+18x+7)/(x^2+x-12)`
`đk:x ne 3,x ne -4`
Nhân 2 vế với `(x-3)(x+4) ne 0` ta có:
`(x+4)^2-(x-3)^2=x^2+18x+7`
`<=>x^2+8x+16-x^2+6x-9=x^2+18x+7`
`<=>14x+7=x^2+18x+7`
`<=>x^2+4x=0`
`<=>x(x+4)=0`
Vì `x ne -4=>x+4 ne 0`
`<=>x=0`
Vậy `S={0}`

Em tách ra mỗi lần hỏi đăng 1-3 bài thôi để nhận hỗ trợ sớm nhất nha em!




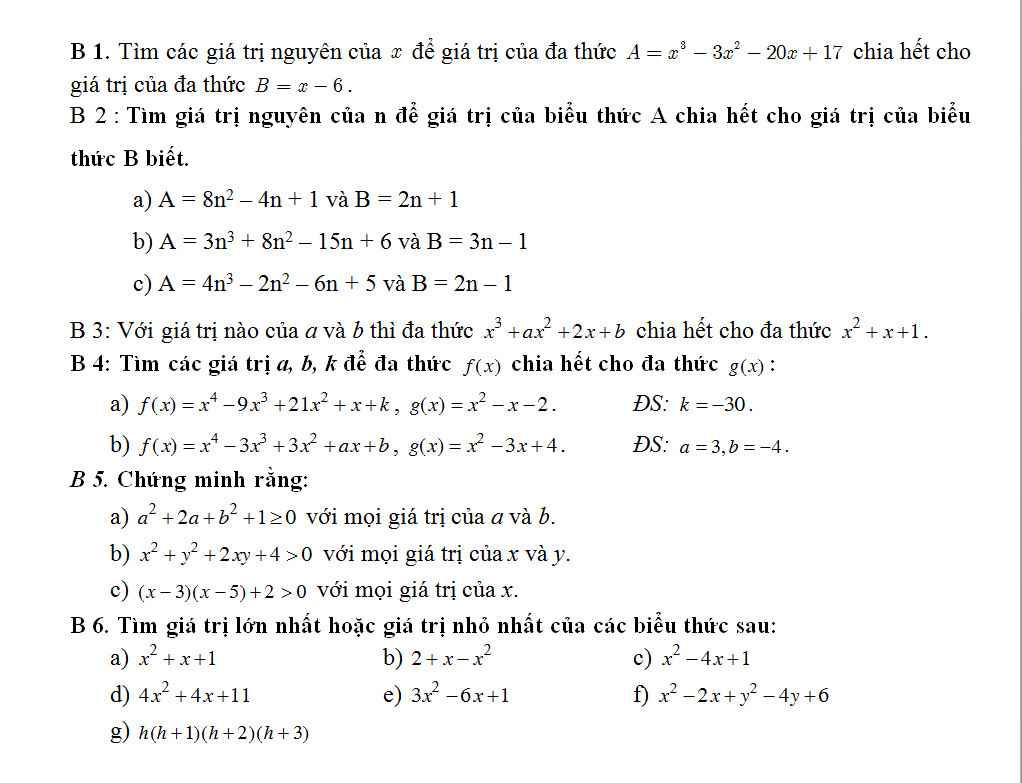



 4 ấy
4 ấy

Trả lời:
Bài 3:
1, \(C=\frac{x-1}{2}:\left(\frac{x^2+2}{x^3-1}+\frac{x}{x^2+x+1}+\frac{1}{1-x}\right)\) \(\left(ĐKXĐ:x\ne1\right)\)
\(=\frac{x-1}{2}:\left(\frac{x^2+2}{x^3-1}+\frac{x}{x^2+x+1}-\frac{1}{x-1}\right)\)
\(=\frac{x-1}{2}:\left(\frac{x^2+2}{\left(x-1\right)\left(x^2+x+1\right)}+\frac{x\left(x-1\right)}{\left(x-1\right)\left(x^2+x+1\right)}-\frac{x^2+x+1}{\left(x-1\right)\left(x^2+x+1\right)}\right)\)
\(=\frac{x-1}{2}:\frac{x^2+2+x\left(x-1\right)-x^2-x-1}{\left(x-1\right)\left(x^2+x+1\right)}\)
\(=\frac{x-1}{2}:\frac{x^2+2+x^2-x-x^2-x-1}{\left(x-1\right)\left(x^2+x+1\right)}\)
\(=\frac{x-1}{2}:\frac{x^2-2x+1}{\left(x-1\right)\left(x^2+x+1\right)}\)
\(=\frac{x-1}{2}:\frac{\left(x-1\right)^2}{\left(x-1\right)\left(x^2+x+1\right)}\)
\(=\frac{x-1}{2}:\frac{x-1}{x^2+x+1}\)
\(=\frac{x-1}{2}\cdot\frac{x^2+x+1}{x-1}=\frac{x^2+x+1}{2}\)
2, Ta có: \(x^2+x+1=\left(x^2+x+\frac{1}{4}\right)+\frac{3}{4}=\left(x+\frac{1}{2}\right)^2+\frac{3}{4}\ge\frac{3}{4}>0\forall x\ne1\)
\(\Rightarrow\frac{x^2+x+1}{2}>0\forall x\ne1\)
Vậy C lớn hơn 0 với mọi x khác 1.
\(1.C=\frac{x-1}{2}:\left(\frac{x^2+2}{\left(x-1\right)\left(x^2+x+1\right)}+\frac{x}{x^2+x+1}+\frac{1}{1-x}\right)\)
\(=\frac{x-1}{2}:\left(\frac{x^2+2+x\left(x-1\right)-\left(x^2+x+1\right)}{\left(x-1\right)\left(x^2+x+1\right)}\right)=\frac{x-1}{2}:\left(\frac{x^2-2x+1}{\left(x-1\right)\left(x^2+x+1\right)}\right)\)
\(=\frac{x-1}{2}.\left(\frac{x^2+x+1}{x-1}\right)=\frac{x^2+x+1}{2}\)
2. ta có : \(C=\frac{x^2+x+\frac{1}{4}}{2}+\frac{3}{8}=\frac{\left(x+\frac{1}{2}\right)^2}{2}+\frac{3}{8}\ge\frac{3}{8}>0\)
3. Vậy GTNN của \(C=\frac{3}{8}\)