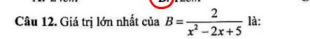K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
RH
15 tháng 12 2021
B lớn nhất khi x^2 - 2x + 5 nhỏ nhất.
Ta có: x^2 - 2x + 5 = (x - 1)^2 + 4 >= 4
--> x^2 - 2x + 5 nhỏ nhất bằng 4 (khi x = 1)
--> B lớn nhất bằng 2/4 = 1/2 (khi x = 1)
L
15 tháng 12 2021
\(B=\dfrac{2}{x^2-2x+5}\)
Ta có:
\(x^2-2x+5\\ =\left(x^2-2x+4\right)-4+5\\ =\left(x-2\right)^2+1\)
Vì \(\left(x+2\right)^2\ge0\forall x\)
\(\Rightarrow\left(x-2\right)^2+1\ge1\forall x\\ \Rightarrow\dfrac{2}{\left(x-2\right)^2+1}\le2\forall x\\ \Rightarrow B\le2\forall x\)
Dấu "=" xảy ra \(\Leftrightarrow\left(x-2\right)^2=0\)
\(\Leftrightarrow x-2=0\\ \Leftrightarrow x=2\)
Vậy GTLN của B là 2 <=> x =2
1 tháng 8 2023
a: N là trung điểm của BC
=>NB=NC=4cm
Xét ΔNAB có NH là phân giác
nên AH/HB=AN/NB=5/4
Xét ΔNAC có NI là phân giác
nên AI/IC=AN/NC=5/4
=>AH/HB=AI/IC
b: Xét ΔABC có AH/HB=AI/IC
nênHI//BC
c: Xét ΔABN có HE//BN
nên HE/BN=AE/AN
Xét ΔACN có EI//NC
nên EI/NC=AE/AN
=>HE/BN=EI/NC
mà BN=NC
nên HE=EI
=>E là trung điểm của HI
d: Sửa đề: ΔABN
Xét ΔAHE và ΔABN có
góc AHE=góc ABN
góc HAE chung
=>ΔAHE đồng dạng với ΔABN
LM
ai giải giúp em mấy bài toán này vs ạ giải chi tiết giúp em ạ
2
10 tháng 11 2021
\(1,\\ a,=6x^4y^4-x^3y^3+\dfrac{1}{2}x^4y^2\\ b,=4x^3+5x^2-8x^2-10x+12x+15\\ =4x^3-3x^2+2x+15\\ 2,\\ a,=7\left(x^2-6x+9\right)=7\left(x-3\right)^2\\ b,=\left(x-y\right)^2-36=\left(x-y-6\right)\left(x-y+6\right)\\ 3,\\ \Leftrightarrow x\left(x^2-0,36\right)=0\\ \Leftrightarrow x\left(x-0,6\right)\left(x+0,6\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x=0,6\\x=-0,6\end{matrix}\right.\)
AD
1
21 tháng 12 2021
nó bị lỗi nên mình làm câu khác rồi
câu hỏi đây nè bạn
Tìm GTLN của \(A=\dfrac{\left(x+2\right)^2}{2}\times\left(1-\dfrac{x^2}{x+2}\right)-\dfrac{x^2+6x+4}{x}\)
NV
1
10 tháng 10 2021
\(P=\dfrac{x^3-y^3}{x^2y-xy^2}-\dfrac{x^3+y^3}{x^2y+xy^2}-\left(\dfrac{x}{y}-\dfrac{y}{x}\right)\left(\dfrac{x+y}{x-y}-\dfrac{x-y}{x+y}\right)\)
\(=\dfrac{\left(x-y\right)\left(x^2+xy+y^2\right)}{xy\left(x-y\right)}-\dfrac{\left(x+y\right)\left(x^2-xy+y^2\right)}{xy\left(x+y\right)}-\dfrac{x^2-y^2}{xy}\cdot\dfrac{x^2+2xy+y^2-x^2+2xy-y^2}{\left(x-y\right)\left(x+y\right)}\)
\(=\dfrac{x^2+xy+y^2-x^2+xy-y^2}{xy}-\dfrac{\left(x-y\right)\left(x+y\right)}{xy}\cdot\dfrac{4xy}{\left(x-y\right)\left(x+y\right)}\)
\(=2-4=-2\)
NV
1
22 tháng 10 2021
a: \(AO=\dfrac{1}{2}AC\)(O là trung điểm của AC)
nên AO=AD
hay ΔAOD cân tại A
NV
Nguyễn Việt Lâm
Giáo viên
11 tháng 11 2021
\(A=-2\left(x^2-\dfrac{1}{2}x\right)=-2\left(x^2-2.x.\dfrac{1}{4}+\dfrac{1}{16}-\dfrac{1}{16}\right)\)
\(=-2\left(x^2-2x.\dfrac{1}{4}+\dfrac{1}{16}\right)+\dfrac{1}{8}=-2\left(x-\dfrac{1}{4}\right)^2+\dfrac{1}{8}\le\dfrac{1}{8}\)
\(\Rightarrow A_{max}=\dfrac{1}{8}\)
