
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Các câu hỏi dưới đây có thể giống với câu hỏi trên
KC
0

SG
1

19 tháng 4 2017
Hướng dẫn:

+ Trên cạnh thứ nhất lấy hai điểm phân biệt A; B trên cạnh thứ hai lấy hai điểm C; D sao cho khoảng cách từ C; D đến đỉnh của góc lần lượt bằng khoảng cách từ đỉnh của góc với A, B
+ Xác định giao điểm I của BC và AD; tia vẽ từ đỉnh của góc qua I chính là tia phân giác của góc đó.
+ Phần chứng minh tương tự như bài 34
19 tháng 4 2017

+ Trên cạnh thứ nhất lấy hai điểm phân biệt A; B trên cạnh thứ hai lấy hai điểm C; D sao cho khoảng cách từ C; D đến đỉnh của góc lần lượt bằng khoảng cách từ đỉnh của góc với A, B
+ Xác định giao điểm I của BC và AD; tia vẽ từ đỉnh của góc qua I chính là tia phân giác của góc đó.
+ Phần chứng minh tương tự như bài 34

18 tháng 5 2022
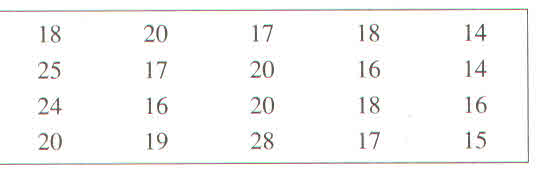
Bài 1:
| Giá trị (x) | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 24 | 25 | 28 | |
| Tần số (n) | 2 | 1 | 3 | 3 | 3 | 1 | 4 | 1 | 1 | 1 | N = 20 |
Bài 2:
| Giá trị (x) | Đỏ | Vàng | Hồng | Trắng | Tím sẫm | Tím nhạt | Xanh da trời | Xanh lá cây | Xanh nước biển | |
| Tần số(n) | 6 | 5 | 4 | 4 | 3 | 3 | 3 | 1 | 1 | N=30 |















Bài 5:
a) Ta có: A+P=Q
nên A=Q-P
\(=2x^2+5xy-3y^2-6x^2+7xy-4y^2\)
\(=-4x^2+12xy-7y^2\)
b) Ta có: B-Q=P
nên B=P+Q
\(=6x^2-7xy+4y^2+2x^2+5xy-3y^2\)
\(=8x^2-2xy+y^2\)
Bài 6:
a) \(P\left(-\dfrac{1}{2}\right)=4\cdot\left(-\dfrac{1}{2}\right)^2-9\cdot\dfrac{-1}{2}=4\cdot\dfrac{1}{4}+\dfrac{9}{2}=1+\dfrac{9}{2}=\dfrac{11}{2}\)
\(Q\left(\dfrac{2}{3}\right)=3\cdot\dfrac{2}{3}+6=2+6=8\)
b) Đặt P(x)=0
\(\Leftrightarrow x\left(4x-9\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=\dfrac{9}{4}\end{matrix}\right.\)
Đặt Q(x)=0
\(\Leftrightarrow3x+6=0\)
hay x=-2
B5:
a)ta có :A+P=Q suy ra A=Q-P
A=-4x^2+12xy-y^2
b)ta có :B-Q=P suy ra A=Q+P
B=8x^2-2xy+y^2