K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
14 tháng 8 2021
Bài 4:
a: Ta có: \(IA=IB=\dfrac{AB}{2}\)
\(DK=KC=\dfrac{DC}{2}\)
mà AB=DC
nên IA=IB=DK=KC
Xét tứ giác IBKD có
IB//DK
IB=DK
Do đó: IBKD là hình bình hành
b: Xét tứ giác AIKD có
AI//DK
AI=DK
Do đó: AIKD là hình bình hành
Suy ra: Hai đường chéo AK và DI cắt nhau tại trung điểm của mỗi đường
mà AK cắt DI tại E
nên E là trung điểm của DI
Suy ra: \(EI=\dfrac{DI}{2}\left(1\right)\)
Xét tứ giác BIKC có
BI//KC
BI=KC
Do đó: BIKC là hình bình hành
Suy ra: Hai đường chéo IC và BK cắt nhau tại trung điểm của mỗi đường
mà IC cắt BK tại F
nên F là trung điểm của BK
\(\Leftrightarrow KF=\dfrac{BK}{2}\left(2\right)\)
Ta có: IBKD là hình bình hành
nên \(ID=BK\left(3\right)\) và ID=BK
Từ \(\left(1\right),\left(2\right),\left(3\right)\) suy ra EI//KF và EI=KF
Xét tứ giác IEKF có
IE//KF
IE=KF
Do đó: IEKF là hình bình hành
14 tháng 8 2021
Bài 4:
c: Xét tứ giác AICK có
AI//CK
AI=CK
Do đó: AICK là hình bình hành
Suy ra: Hai đường chéo AC và IK cắt nhau tại trung điểm của mỗi đường\(\left(4\right)\)
Ta có: EIFK là hình bình hành
nên hai đường chéo EF và IK cắt nhau tại trung điểm của mỗi đường\(\left(5\right)\)
Từ \(\left(4\right),\left(5\right)\) suy ra AC,EF,IK đồng quy
NT
3
HT
0
26 tháng 11 2023
Bài III:
a: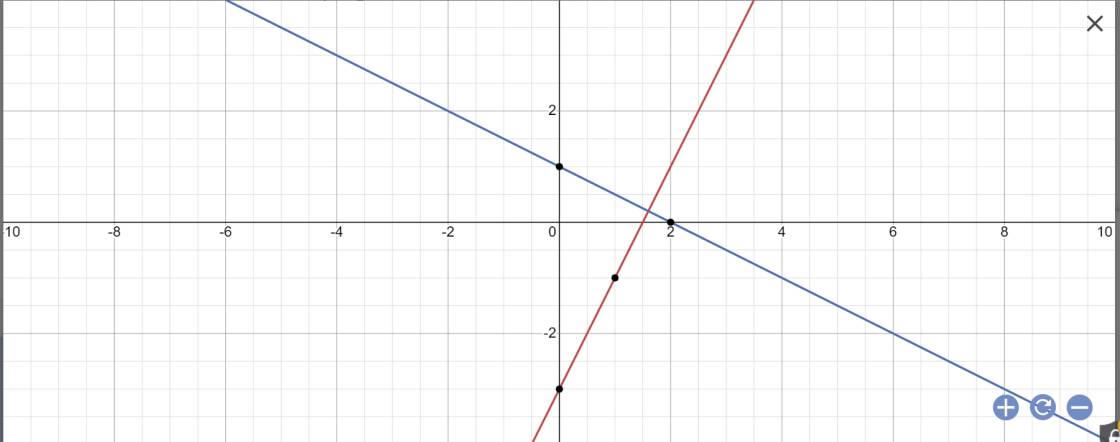 
b: Phương trình hoành độ giao điểm là:
\(2x-3=-\dfrac{1}{2}x+1\)
=>\(2x+\dfrac{1}{2}x=3+1\)
=>\(\dfrac{5}{2}x=4\)
=>\(x=4:\dfrac{5}{2}=4\cdot\dfrac{2}{5}=\dfrac{8}{5}\)
Khi x=8/5 thì \(y=2x-3=2\cdot\dfrac{8}{5}-3=\dfrac{16}{5}-3=\dfrac{1}{5}\)
Vậy: tọa độ giao điểm của (d) và (d') là \(B\left(\dfrac{8}{5};\dfrac{1}{5}\right)\)
c: Vì (m)//(d) nên \(\left\{{}\begin{matrix}a=2\\b< >-3\end{matrix}\right.\)
Vậy: (m): \(y=2x+b\)
Thay x=-2 và y=2 vào (m), ta được:
\(b+2\cdot\left(-2\right)=2\)
=>b-4=2
=>b=6
Vậy: (m): y=2x+6
9 tháng 10 2021
\(3,\\ a,ĐK:x\ge-5\\ PT\Leftrightarrow2\sqrt{x+5}-2\sqrt{x+5}+3\sqrt{x+5}=12\\ \Leftrightarrow\sqrt{x+5}=4\Leftrightarrow x+5=16\Leftrightarrow x=11\left(tm\right)\\ b,ĐK:x\in R\\ PT\Leftrightarrow\left|x-5\right|=6\Leftrightarrow\left[{}\begin{matrix}x-5=6\\5-x=6\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=11\\x=-1\end{matrix}\right.\)
29 tháng 7 2021
Bài 4:
a, \(\sqrt{3x+4}-\sqrt{2x+1}=\sqrt{x+3}\) (ĐK: \(x\ge\dfrac{-1}{2}\))
\(\Rightarrow\) \(\left(\sqrt{3x+4}-\sqrt{2x+1}\right)^2\) = x + 3
\(\Leftrightarrow\) \(3x+4+2x+1-2\sqrt{\left(3x+4\right)\left(2x+1\right)}=x+3\)
\(\Leftrightarrow\) \(4x+2=2\sqrt{6x^2+11x+4}\)
\(\Leftrightarrow\) \(2x+1=\sqrt{6x^2+11x+4}\)
\(\Rightarrow\) \(4x^2+4x+1=6x^2+11x+4\)
\(\Leftrightarrow\) \(2x^2+7x+3=0\)
\(\Delta=7^2-4.2.3=25\); \(\sqrt{\Delta}=5\)
Vì \(\Delta\) > 0; theo hệ thức Vi-ét ta có:
\(x_1=\dfrac{-7+5}{4}=\dfrac{-1}{2}\)(TM); \(x_2=\dfrac{-7-5}{4}=-3\) (KTM)
Vậy ...
Các phần còn lại bạn làm tương tự nha, phần d bạn chuyển \(-\sqrt{2x+4}\) sang vế trái rồi bình phương 2 vế như bình thường là được
Bài 5:
a, \(\sqrt{x+4\sqrt{x}+4}=5x+2\)
\(\Leftrightarrow\) \(\sqrt{\left(\sqrt{x}+2\right)^2}=5x+2\)
\(\Rightarrow\) \(\sqrt{x}+2=5x+2\)
\(\Leftrightarrow\) \(5x-\sqrt{x}=0\)
\(\Leftrightarrow\) \(\sqrt{x}\left(5\sqrt{x}-1\right)=0\)
\(\Leftrightarrow\) \(\left[{}\begin{matrix}\sqrt{x}=0\\5\sqrt{x}-1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=\dfrac{1}{25}\end{matrix}\right.\)
Vậy ...
Phần b cũng là hằng đẳng thức thôi nha \(\sqrt{x^2-2x+1}=\sqrt{\left(x-1\right)^2}=x-1\); \(\sqrt{x^2+4x+4}=\sqrt{\left(x+2\right)^2}=x+2\) rồi giải như bình thường là xong nha!
VD1:
a, \(\sqrt{2x-1}=\sqrt{2}-1\) (x \(\ge\) \(\dfrac{1}{2}\))
\(\Leftrightarrow\) \(2x-1=\left(\sqrt{2}-1\right)^2\) (Bình phương 2 vế)
\(\Leftrightarrow\) \(2x-1=2-2\sqrt{2}+1\)
\(\Leftrightarrow\) \(2x=4-2\sqrt{2}\)
\(\Leftrightarrow\) \(x=2-\sqrt{2}\) (TM)
Vậy ...
Phần b tương tự nha
c, \(\sqrt{3}x^2-\sqrt{12}=0\)
\(\Leftrightarrow\) \(\sqrt{3}x^2=\sqrt{12}\)
\(\Leftrightarrow\) \(x^2=2\)
\(\Leftrightarrow\) \(x=\pm\sqrt{2}\)
Vậy ...
d, \(\sqrt{2}\left(x-1\right)-\sqrt{50}=0\)
\(\Leftrightarrow\) \(\sqrt{2}\left(x-1\right)=\sqrt{50}\)
\(\Leftrightarrow\) \(x-1=5\)
\(\Leftrightarrow\) \(x=6\)
Vậy ...
VD2:
Phần a dễ r nha (Bình phương 2 vế rồi tìm x như bình thường)
b, \(\sqrt{x^2-x}=\sqrt{3-x}\) (\(x\le3\); \(x^2\ge x\))
\(\Leftrightarrow\) \(x^2-x=3-x\) (Bình phương 2 vế)
\(\Leftrightarrow\) \(x^2=3\)
\(\Leftrightarrow\) \(x=\pm\sqrt{3}\) (TM)
Vậy ...
c, \(\sqrt{2x^2-3}=\sqrt{4x-3}\) (x \(\ge\) \(\dfrac{\sqrt{3}}{2}\))
\(\Leftrightarrow\) \(2x^2-3=4x-3\) (Bình phương 2 vế)
\(\Leftrightarrow\) \(2x^2-4x=0\)
\(\Leftrightarrow\) \(2x\left(x-2\right)=0\)
\(\Leftrightarrow\) \(\left[{}\begin{matrix}2x=0\\x-2=0\end{matrix}\right.\)
\(\Leftrightarrow\) \(\left[{}\begin{matrix}x=0\left(KTM\right)\\x=2\left(TM\right)\end{matrix}\right.\)
Vậy ...
Chúc bn học tốt! (Có gì không biết cứ hỏi mình nha!)
Ai giúp em với ạ em cần rất gấp bài 4 thôi ạ
4 tháng 10 2021
3: Ta có: ΔABC vuông tại A
nên \(\widehat{B}+\widehat{C}=90^0\)
hay \(\widehat{B}=60^0\)
Xét ΔABC vuông tại A có
\(\sin\widehat{C}=\dfrac{AB}{BC}\)
\(\Leftrightarrow AB=12.5\left(cm\right)\)
\(\Leftrightarrow AC=12.5\sqrt{3}\left(cm\right)\)