
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(1,\\ a,=5x^2-3xy+1\\ b,=\dfrac{x^2-3x}{2x-6}=\dfrac{x\left(x-3\right)}{2\left(x-3\right)}=\dfrac{x}{2}\\ c,=\dfrac{2x}{x+5}\cdot\dfrac{\left(x-5\right)\left(x+5\right)}{6x^2}=\dfrac{x-5}{3x}\\ 2,\\ a,\Leftrightarrow\left(x+3-4\right)\left(x+3+4\right)=0\\ \Leftrightarrow\left(x-1\right)\left(x+7\right)=0\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-7\end{matrix}\right.\\ b,\left(5n+2\right)^2-4=\left(5n+2+2\right)\left(5n+2-2\right)=5n\left(5n+4\right)⋮5\left(5⋮5\right)\)

1: \(x^2-2x+1=\left(x-1\right)^2\)
2: \(4x^2-4x+1=\left(2x-1\right)^2\)
3: \(16x^2+8x+1=\left(4x+1\right)^2\)
4: \(9x^2+12x+4=\left(3x+2\right)^2\)
5: \(x^2-x+\dfrac{1}{4}=\left(x-\dfrac{1}{2}\right)^2\)

84. Cho tam giác ABC, D là điểm nằm giữa B và C. Qua D kẻ các đường thẳng song song với AB và AC, chúng cắt các cạnh AC và AB theo thứ tự ở E và F.
a) Tứ giác AEDF là hình gi ? Vì sao ?
b) Điểm D ở vị trí nào trên cạnh BC thì tứ giác AEDF là hình thoi ?
c) Nếu tam giác ABC vuông tại A thì tứ giác AEDF là hình gì ? Điểm D ở vị trí nào trên cạnh BC thì tứ giác AEDF là hình vuông ?
Bài giải:
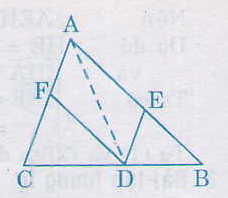
a) Tứ giác AEDF là hình bình hành.
Vì có DE // AF, DF // AE (gt)
(theo định nghĩa)
b) Hình bình hành AEDF là hình thoi khi AD là tia phân giác của góc A với cạnh BC thì AEDF là hình thoi.
c) Nếu ∆ABC vuông tại A thì AEDF là hình chữ nhật (vì là hình bình hành có một góc vuông).
Nếu ABC vuông tại A và D là giao điểm của tia phân giác của góc A với cạnh BC thì AEDF là hình vuông (vì vừa là hình chữ nhật vừa là hình thoi).

Bài b) (x-4)(x-7)(x-6)(x-5)=1680
=> (x2-11x+28)(x2-11x+30)=1680
Đặt t=x2-11x+28
=> t(t+2)=1680
=>t2+2t-1680=0
=> t2+2t+1-1681=0
=> (t+1)2-412=0
=> (t-40)(t+42)=0
=> t=40 hoặc t=-42
Bạn thế vào như câu a) để giải nhé !!!


( x+2)(x+5)(x+4)(x+3) = 24
<=> (x2 + 5x + 2x + 10)( x2 + 3x+4x+12 ) = 24
<=> ( x2 +7x+10)(x2+7x+12) = 24
Đặt x2 + 7x = t
Thay t vào phương trình , ta có
( t + 10)(t+12) = 24
<=> t2 + 12t + 10t + 120 - 24 = 0
<=> t2 + 22t + 96 = 0
<=> t2 + 6t + 16t + 96 = 0
<=> t( t+6)+16(t+6) = 0
<=> (t+16)(t+6) = 0
=> t+ 16 = 0 => t= -16
hoặc t+6=0 => t= - 6
rồi từ đó giải phương trình x2+ 7x = -16 và phương trình x2+7x = -6
x là tất cả các giá trị tìm được

gọi a;b;c;d lần lượt là số t1;t2;t3;t4
ta có pt: a+2/54=b-2/54=c/108=d/27=a+2+b-2+c+d/54+54+108+27=54/243=2/9
=>a=2/9 x 54 - 2=10
b=2/9 x 54 + 2=14
c=2/9 x 108=24
d=2/9 x 27=6

nếu tìm x thì mk làm đc:
\(\frac{x}{3}+\frac{2x-6}{6}=2-\frac{x}{3}\)
\(\Leftrightarrow\frac{2x}{6}+\frac{2x-6}{6}=\frac{6}{x}-\frac{x}{3}\)
\(\Leftrightarrow\frac{2x+2x-6}{6}=\frac{6-x}{3}\)
\(\Leftrightarrow\frac{2x+2x-6}{6}=\frac{2\left(6-x\right)}{2.3}=\frac{12-2x}{6}\)
<=>2x+2x-6=12-2x
<=>4x-6=12-2x
<=>4x-2x=12-6
<=>2x=6<=>x=3
Vậy x=3

 Ai giải hộ mình bài 18 với! Mình đang cần gấp lắm :(( Cảm ơn trước nha
Ai giải hộ mình bài 18 với! Mình đang cần gấp lắm :(( Cảm ơn trước nha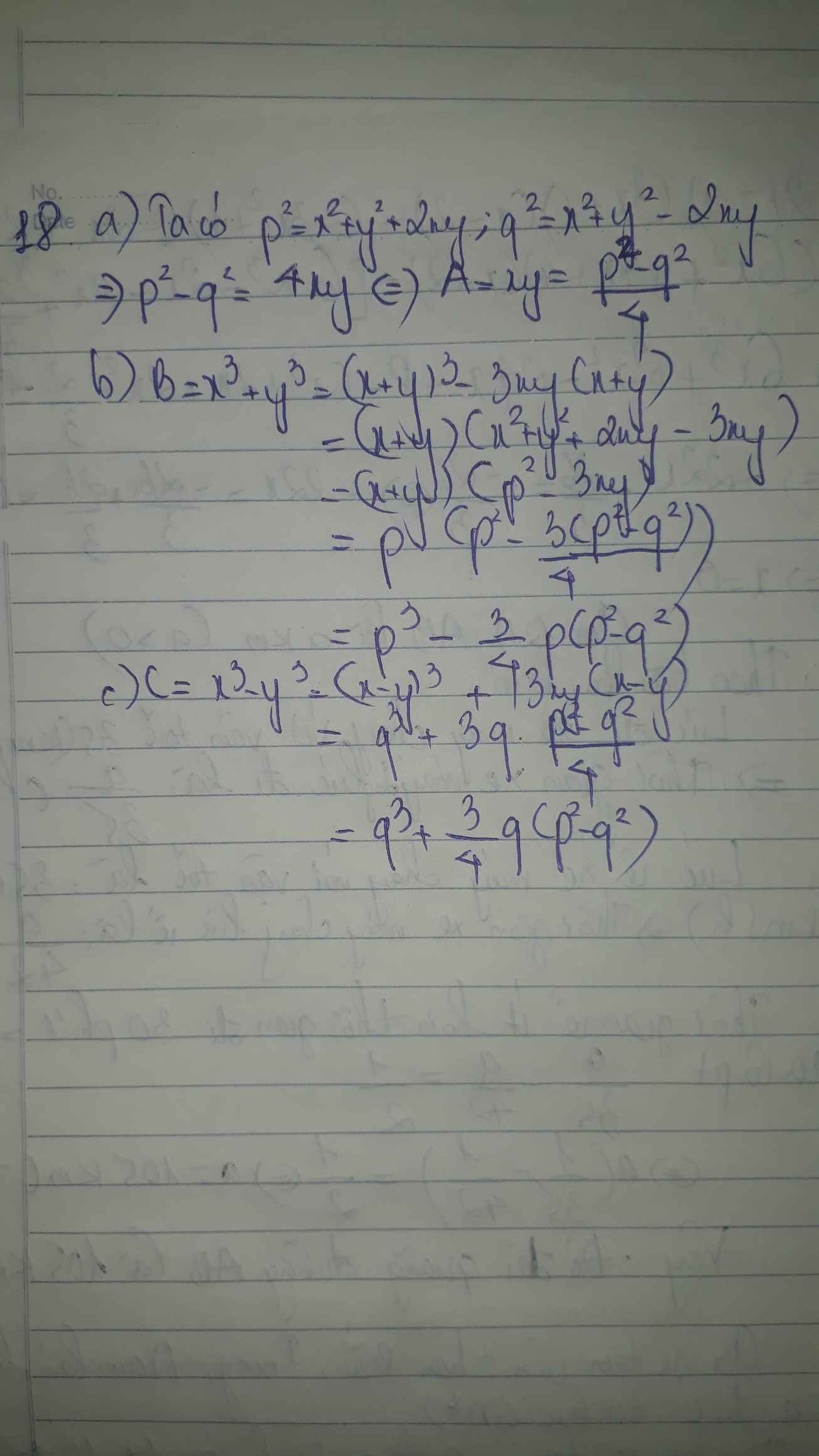


4:
1: Xét ΔHKB vuông tại K và ΔHIC vuông tại I có
\(\widehat{KHB}=\widehat{CHI}\)(hai góc đối đỉnh)
Do đó: ΔKHB~ΔIHC
2: Ta có: ΔKHB~ΔIHC
=>\(\widehat{HBK}=\widehat{HCI}\)
=>\(\widehat{ICH}=\widehat{IBC}\)
Xét ΔICH vuông tại I và ΔIBC vuông tại I có
\(\widehat{ICH}=\widehat{IBC}\)
Do đó: ΔICH~ΔIBC
=>\(\dfrac{IC}{IB}=\dfrac{IH}{IC}\)
=>\(IC^2=IH\cdot IB\)
3: Xét ΔCAB có
CK,BI là các đường cao
CK cắt BI tại H
Do đó: H là trực tâm của ΔCAB
=>AH\(\perp\)BC tại D
Xét tứ giác AIHK có \(\widehat{AIH}+\widehat{AKH}=90^0+90^0=180^0\)
nên AIHK là tứ giác nội tiếp
Xét tứ giác BKHD có \(\widehat{BKH}+\widehat{BDH}=90^0+90^0=180^0\)
nên BKHD là tứ giác nội tiếp
Ta có: \(\widehat{IKH}=\widehat{IAH}\)(AIHK nội tiếp)
\(\widehat{DKH}=\widehat{DBH}\)(BKHD nội tiếp)
mà \(\widehat{IAH}=\widehat{DBH}\left(=90^0-\widehat{ACD}\right)\)
nên \(\widehat{IKH}=\widehat{DKH}\)
=>KH là phân giác của góc IKD