
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


5.1) Gọi \(A\left(x_A;y_A\right)\) là giao điểm của \(\left(d_1\right)\) và \(\left(d_2\right)\)
\(\Rightarrow\left\{{}\begin{matrix}y_A=2x_A+1\\y_A=-x_A+3\end{matrix}\right.\Rightarrow2x_A+1=-x_A+3\Rightarrow3x_A=2\Rightarrow x_A=\dfrac{2}{3}\)
\(\Rightarrow y_A=\dfrac{7}{3}\Rightarrow A\left(\dfrac{2}{3};\dfrac{7}{3}\right)\)
2) Vì \(\left(d_3\right)\) đi qua A nên \(\dfrac{7}{3}=\dfrac{2}{3}\left(m-1\right)+3m-2\Rightarrow\dfrac{7}{3}=\dfrac{11}{3}m-\dfrac{8}{3}\)
\(\Rightarrow\dfrac{11}{3}m=5\Rightarrow m=\dfrac{15}{11}\)
3) Gọi \(B\left(x_B;y_B\right)\) là giao điểm của \(\left(d_1\right)\) và \(\left(d_3\right)\)
Vì \(B\in Ox\Rightarrow y_B=0\)
Vì \(B\in\left(d_1\right)\Rightarrow y_B=2x_B+1\Rightarrow0=2x_B+1\Rightarrow x_B=-\dfrac{1}{2}\)
\(\Rightarrow B\left(-\dfrac{1}{2};0\right)\Rightarrow0=-\dfrac{1}{2}\left(m-1\right)+3m-2\Rightarrow0=\dfrac{5}{2}m-\dfrac{3}{2}\)
\(\Rightarrow\dfrac{5}{2}m=\dfrac{3}{2}\Rightarrow m=\dfrac{3}{5}\)
c) Gọi \(C\left(x_C;y_C\right)\) là giao điểm của \(\left(d_2\right)\) và \(\left(d_3\right)\)
Vì \(C\in Oy\Rightarrow x_C=0\)
Vì \(B\in\left(d_2\right)\Rightarrow y_B=-x_B+3\Rightarrow y_B=3\Rightarrow C\left(0;3\right)\)
\(\Rightarrow3=3m-2\Rightarrow3m=5\Rightarrow m=\dfrac{5}{3}\)


Câu 2: b. \(\sqrt{9x^2-6x+1}=9\)
<=> \(\sqrt{\left(3x-1\right)^2}=9\)
<=> 3x - 1 = 9
<=> 3x = 10
<=> x = \(\dfrac{10}{3}\)

\(A=\frac{\sqrt{5-2\sqrt{5}\sqrt{3}+3}}{\sqrt{10}-\sqrt{6}}\)
\(A=\frac{\sqrt{\left(\sqrt{5}-\sqrt{3}\right)^2}}{\sqrt{10}-\sqrt{6}}\)
\(A=\frac{\sqrt{5}-\sqrt{3}}{\sqrt{10}-\sqrt{6}}\)
\(A=\frac{\sqrt{5}-\sqrt{3}}{\sqrt{2}\left(\sqrt{5}-\sqrt{3}\right)}\)
\(A=\frac{1}{\sqrt{2}}\)
\(A=\frac{\sqrt{\left(\sqrt{5}\right)^2-2\sqrt{5}\sqrt{3}+\left(\sqrt{3}\right)^2}}{\sqrt{2}\left(\sqrt{5}-\sqrt{3}\right)}=\frac{\sqrt{\left(\sqrt{5}-\sqrt{3}\right)^2}}{\sqrt{2}\left(\sqrt{5}-\sqrt{3}\right)}=\frac{\left(\sqrt{5}-\sqrt{3}\right)}{\sqrt{2}\left(\sqrt{5}-\sqrt{3}\right)}=\frac{1}{\sqrt{2}}\\ \)

Bài 1:
3: ĐKXĐ: x>=1
\(x-\sqrt{x+3+4\sqrt{x-1}}=1\)
=>\(x-\sqrt{x-1+2\cdot\sqrt{x-1}\cdot2+4}=1\)
=>\(x-\sqrt{\left(\sqrt{x-1}+2\right)^2}=1\)
=>\(x-\left|\sqrt{x-1}+2\right|=1\)
=>\(x-\left(\sqrt{x-1}+2\right)=1\)
=>\(x-\sqrt{x-1}-2-1=0\)
=>\(x-1-\sqrt{x-1}-2=0\)
=>\(\left(\sqrt{x-1}\right)^2-2\sqrt{x-1}+\sqrt{x-1}-2=0\)
=>\(\left(\sqrt{x-1}-2\right)\left(\sqrt{x-1}+1\right)=0\)
=>\(\sqrt{x-1}-2=0\)
=>\(\sqrt{x-1}=2\)
=>x-1=4
=>x=5(nhận)

11.
\(=\frac{\sqrt{x}-3}{2-\sqrt{x}}+\frac{\sqrt{x}-2}{3+\sqrt{x}}+\frac{9-x}{(2-\sqrt{x})(\sqrt{x}+3)}\)
\(=\frac{(\sqrt{x}-3)(\sqrt{x}+3)}{(2-\sqrt{x})(\sqrt{x}+3)}+\frac{\sqrt{x}-2}{3+\sqrt{x}}+\frac{9-x}{(2-\sqrt{x})(\sqrt{x}+3)}\)
\(=\frac{x-9}{(2-\sqrt{x})(\sqrt{x}+3)}+\frac{\sqrt{x}-2}{3+\sqrt{x}}+\frac{9-x}{(2-\sqrt{x})(\sqrt{x}+3)}\)
\(=\frac{\sqrt{x}-2}{3+\sqrt{x}}\)
12.
\(=\frac{(3-\sqrt{x})(3\sqrt{x}-2)+(5\sqrt{x}+7)(3\sqrt{x}+4)}{(5\sqrt{x}+7)(3\sqrt{x}-2)}-\frac{42\sqrt{x}+34}{(5\sqrt{x}+7)(3\sqrt{x}-2)}\)
\(=\frac{12x+52\sqrt{x}+22}{(5\sqrt{x}+7)(3\sqrt{x}-2)}-\frac{42\sqrt{x}+34}{(5\sqrt{x}+7)(3\sqrt{x}-2)}\)
\(=\frac{12x+10\sqrt{x}-12}{(5\sqrt{x}+7)(3\sqrt{x}-2)}=\frac{2(3\sqrt{x}-2)(2\sqrt{x}+3)}{(5\sqrt{x}+7)(3\sqrt{x}-2)}=\frac{2(2\sqrt{x}+3)}{5\sqrt{x}+7}\)

a: Xét ΔAHB vuông tại H có HE là đường cao ứng với cạnh huyền AB, ta được:
\(AE\cdot AB=AH^2\left(1\right)\)
Xét ΔHAC vuông tại H có HF là đường cao ứng với cạnh huyền AC, ta được:
\(AF\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AE\cdot AB=AF\cdot AC\)
hay \(\dfrac{AE}{AC}=\dfrac{AF}{AB}\)
Xét ΔAEF vuông tại A và ΔACB vuông tại A có
\(\dfrac{AE}{AC}=\dfrac{AF}{AB}\)
Do đó: ΔAEF\(\sim\)ΔACB
Suy ra: \(\widehat{AEF}=\widehat{ACB}\)



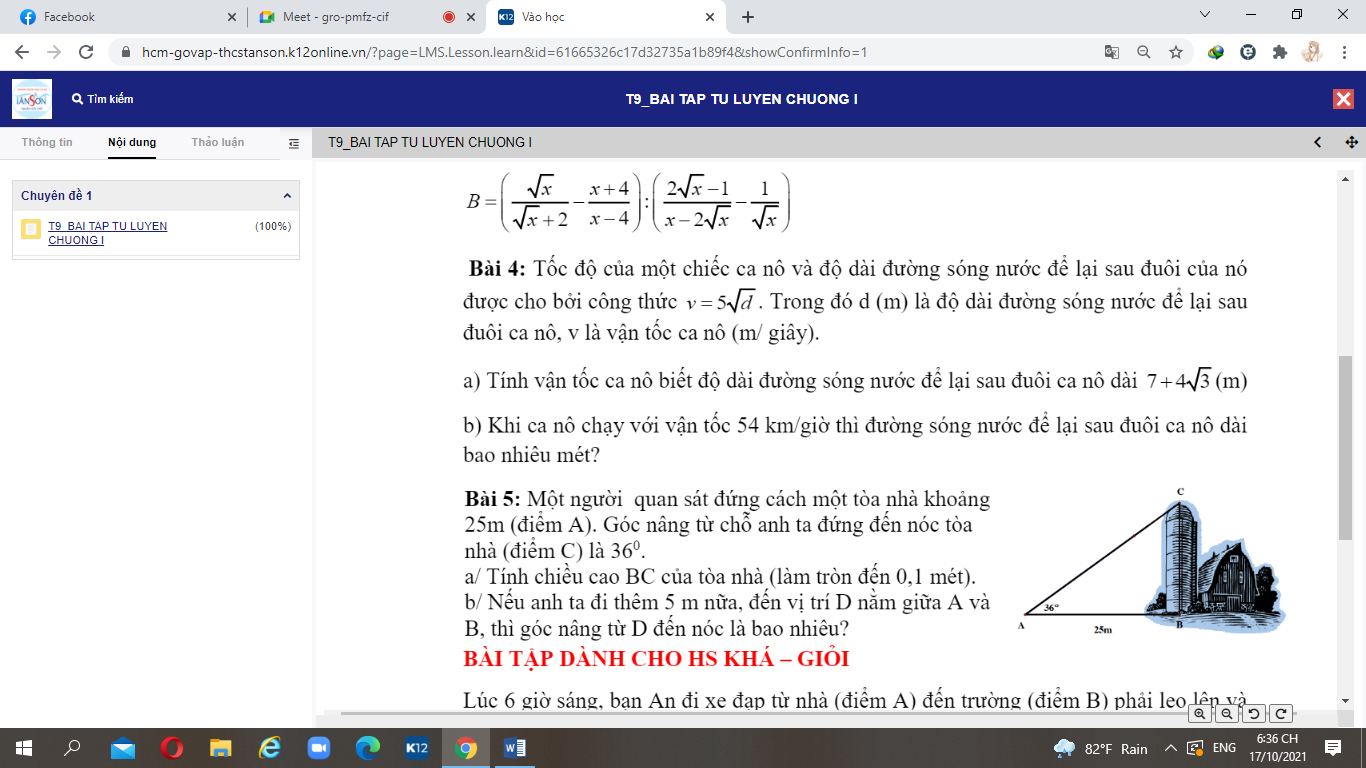
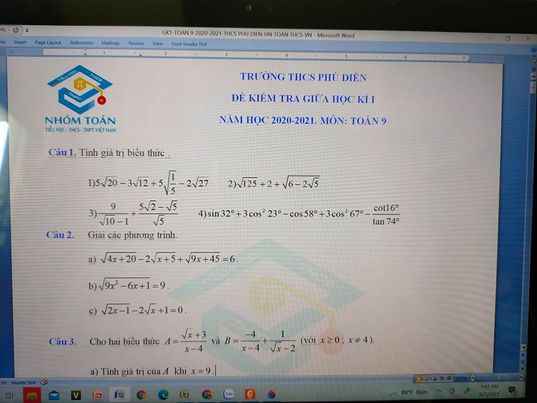 Giải giúp mình bài 1 bài 2 đi mn
Giải giúp mình bài 1 bài 2 đi mn
 giải giúp em bài 11 12 13 của bài 14 đi ạ
giải giúp em bài 11 12 13 của bài 14 đi ạ