K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
13 tháng 3 2017
Ta có:\(\left(-5a^2b^4c^6\right)^7-\left(9a^3bc^5\right)^8=0\)
\(\left(-5\right)^7a^{14}b^{28}c^{42}-9^8a^{24}b^8c^{40}=0\)
Vì \(a^{14}b^{28}c^{42}\ge0\Rightarrow\left(-5\right)^7a^{14}b^{28}c^{42}\le0\)
\(a^{24}b^8c^{40}\ge0\Rightarrow9^8a^{24}b^8c^{40}\ge0\)
\(\Rightarrow\left(-5\right)^7a^{14}b^{28}c^{42}-9^8a^{24}b^8c^{40}\le0\)
Mà VP=0
Dấu "=" xảy ra khi
\(\left(-5\right)^7a^{14}b^{28}c^{42}=0\) và \(9^8a^{24}b^8c^{40}=0\)
\(\Rightarrow a=b=c=0\)
\(\Rightarrow A=a+b+c=0+0+0=0\)
19 tháng 3 2017
Ta có:
(22x + 3y) - (12x - 7y) = 1 - (-9)
22x + 3y - 12x + 7y = 1+ 9
10x + 10y = 10
10 (x + y) = 10
x + y = 10 : 10 = 1
=> Trung bình cộng của x và y bằng 1 : 2 = 0.5
23 tháng 3 2017
=1+\(\dfrac{1}{2}\).3+\(\dfrac{1}{3}\).6+\(\dfrac{1}{4}\).10+....+\(\dfrac{1}{16}\).136
= 1+\(\dfrac{3}{2}\)+2+\(\dfrac{5}{2}\)+..+\(\dfrac{17}{2}\)
=(1+2+...+8)+(\(\dfrac{3}{2}\)+\(\dfrac{5}{2}\)+..+\(\dfrac{17}{2}\))
= 36+40=76
H
17 tháng 3 2017
Để biểu thức P đạt giá trị lớn nhất thì mẫu phải đạt GTNN.
\(\Rightarrow5+x^2\) phải nhỏ nhất
\(\Rightarrow x^2\) phải nhỏ nhất
mà \(x^2\ge0\)
\(\Rightarrow x^2\) nhỏ nhất là bằng 0
\(\Rightarrow x=0\)
Vậy thì tick cho mik nhé!!!
AT
17 tháng 3 2017
Có:\(\dfrac{x}{y}=\dfrac{2}{3}\Rightarrow\dfrac{x}{2}=\dfrac{y}{3}\Rightarrow\dfrac{x}{6}=\dfrac{y}{9}\)
\(\dfrac{x}{3}=\dfrac{z}{5}\Rightarrow\dfrac{x}{6}=\dfrac{x}{10}\)
\(\Rightarrow\dfrac{x}{6}=\dfrac{y}{9}=\dfrac{z}{10}\Rightarrow\dfrac{x^2}{36}=\dfrac{y^2}{81}=\dfrac{z^2}{100}\)
và \(x^2+y^2+z^2=\dfrac{217}{4}\)
Áp dụng t/c của dãy tỉ số = nhau ta có:
\(\dfrac{x^2}{36}=\dfrac{y^2}{81}=\dfrac{z^2}{100}=\dfrac{x^2+y^2+z^2}{36+81+100}=\dfrac{217}{\dfrac{4}{217}}=\dfrac{217}{4.217}=0,25\)
\(\Rightarrow\left[{}\begin{matrix}x^2=9\\y^2=20,25\\z^2=25\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=3\\y=4,5\\z=5\end{matrix}\right.\)
(mk chỉ lấy x,y,z t/m đề thoy)
\(\Rightarrow x+2y-2z=3+2\cdot4,5-2\cdot5=2\)
Vậy............................
H
17 tháng 3 2017
Có: \(\dfrac{a}{3}=\dfrac{b}{5}\)
\(=\dfrac{3a}{3.3}=\dfrac{b}{5}\)
\(=\dfrac{3a}{9}=\dfrac{b}{5}=\dfrac{3a+b}{9+5}=\dfrac{2}{14}=\dfrac{1}{7}\)
\(\Rightarrow\dfrac{a}{3}=\dfrac{1}{7}\Rightarrow a=\dfrac{\left(1.3\right)}{7}=\dfrac{3}{7}\)
Vậy số a thỏa mãn là \(\dfrac{3}{7}\)
Tick nha!!!
H
17 tháng 3 2017
Có: \(\dfrac{a}{3}=\dfrac{b}{3}=\dfrac{c}{4}\)
\(\Rightarrow\dfrac{a^3}{2^3}=\dfrac{b^3}{3^3}=\dfrac{c^3}{4^3}\)
\(=\dfrac{a^3}{8}=\dfrac{b^3}{27}=\dfrac{c^3}{64}\)
\(=\dfrac{a^3+b^3+c^3}{8+27+64}=\dfrac{792}{99}=8\)
\(\Rightarrow\dfrac{a^3}{8}=8\Rightarrow a^3=8.8=64\)
\(\Rightarrow a=4\)
\(\dfrac{b^3}{27}=8\Rightarrow b^3=8.27=216\)
\(\Rightarrow b=6\)
\(\dfrac{c^3}{64}=8\Rightarrow c^3=8.64=512\)
\(\Rightarrow c=8\)
Vậy giá trị của biểu thức \(H=\left|a+b-c\right|=\left|4+6-8\right|=\left|2\right|=2\)
Tick mik nha!!!
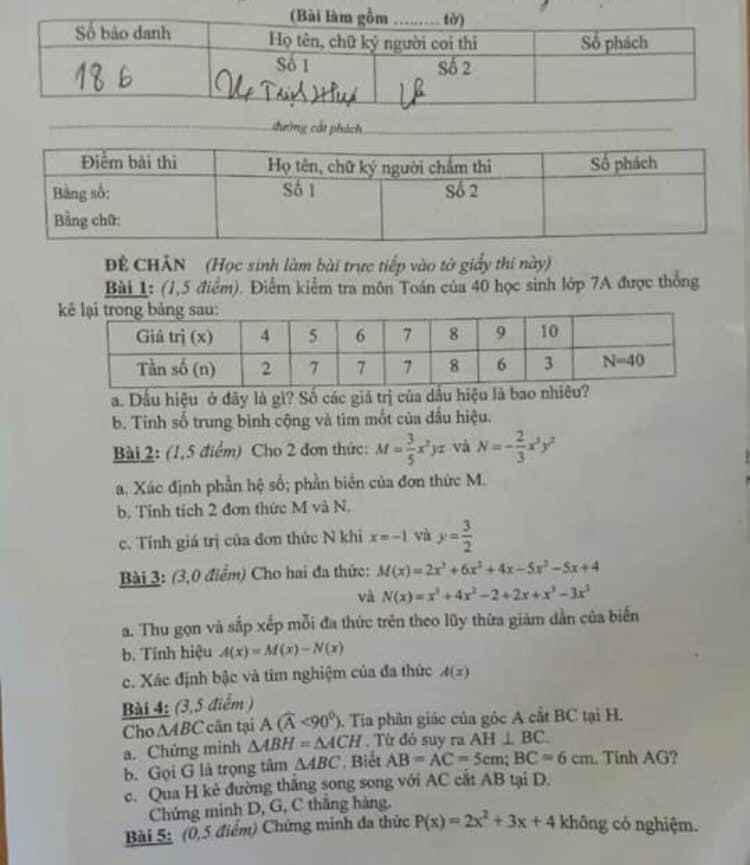
Bài 1:
a) Dấu hiệu: Điểm kiểm tra môn toán của 40 học sinh lớp 7A
số các giá trị: 40
b) số trung bình cộng: (4.2+5.7+6.7+7.7+8.8+9.6+10.3)/40=7,05
M0= 8