
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
JW
1

Các câu hỏi dưới đây có thể giống với câu hỏi trên
SG
1

HN
24 tháng 5 2017
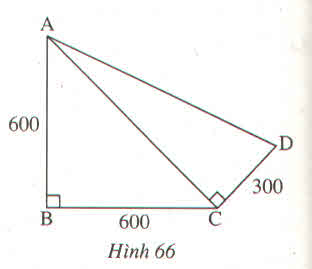
\(\Delta ABC\) vuông tại B. Theo định lí Py-ta-go:
AC2 = AB2 + BC2 = 6002 + 6002 = 360000 + 360000 = 720000.
\(\Delta ACD\) vuông tại C. Theo định lí Py-ta-go:
AD2 = AC2 + CD2 = 720000 + 3002 = 720000 + 90000 = 810000 = 9002 .
Suy ra: AD = 900m.
Quãng đường ABC dài: 600 + 600 = 1200 (m)
Quãng đường CDA dài: 300 + 900 = 1200 (m)
Vậy quãng đường lúc đi bằng quãng đường lúc về.
KC
0

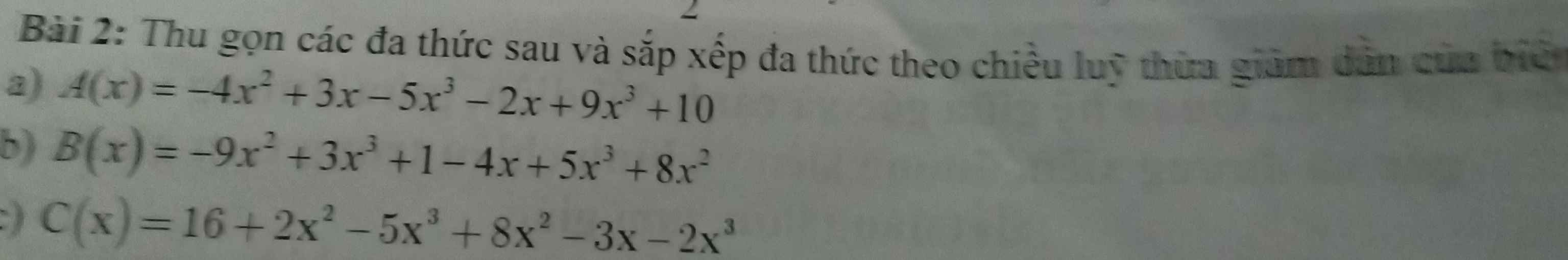












\(A\left(x\right)=4x^3-4x^2+x+10\)
\(B\left(x\right)=8x^3-x^2-4x+1\)
\(C\left(x\right)=-7x^3+10x^2-3x+16\)