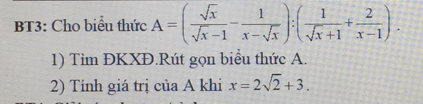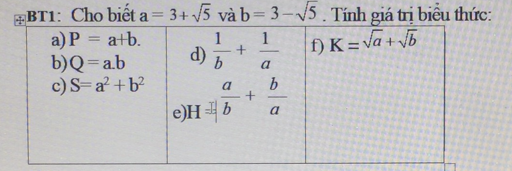K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
TH
2
13 tháng 9 2019
ko đăng linh tinh nha bạn
còn cách gì đó lên mạng mà tìm
KV
10 tháng 12 2023
K = a² - 2ab + 5b² - 4b + 9
= (a² - 2ab + b²) + (4b² - 4b + 1) + 8
= (a - b)² + (2b - 1)² + 8
Do (a - b)² ≥ 0 với mọi a, b ∈ R
(2b - 1)² ≥ 0 với mọi b R
⇒ (a - b)² + (2b - 1)² ≥ 0 với mọi a, b ∈ R
⇒ (a - b)² + (2b - 1)² + 8 ≥ 8 với mọi a, b ∈ R
Vậy GTNN của K là 8 khi a = b = 1/2
BH
1
29 tháng 1
Bài 7:
a: ĐKXĐ: \(x\notin\left\{\dfrac{1}{2};-5\right\}\)
\(\dfrac{x+5}{2x-1}-\dfrac{1-2x}{x+5}-2=0\)
=>\(\dfrac{x+5}{2x-1}+\dfrac{2x-1}{x+5}-2=0\)
=>\(\dfrac{\left(x+5\right)^2+\left(2x-1\right)^2}{\left(2x-1\right)\left(x+5\right)}=2\)
=>\(\left(x+5\right)^2+\left(2x-1\right)^2=2\left(2x-1\right)\left(x+5\right)\)
=>\(x^2+10x+25+4x^2-4x+1=2\left(2x^2+10x-x-5\right)\)
=>\(5x^2+6x+26-4x^2-18x+10=0\)
=>\(x^2-12x+36=0\)
=>\(\left(x-6\right)^2=0\)
=>x-6=0
=>x=6(nhận)
b: ĐKXĐ: \(x\notin\left\{3;-2;4\right\}\)
\(1-\dfrac{8}{x-4}=\dfrac{5}{3-x}-\dfrac{8-x}{x+2}\)
=>\(\dfrac{x-4-8}{x-4}=\dfrac{-5}{x-3}+\dfrac{x-8}{x+2}\)
=>\(\dfrac{x-12}{x-4}=\dfrac{-5\left(x+2\right)+\left(x-8\right)\left(x-3\right)}{\left(x-3\right)\left(x+2\right)}\)
=>\(\dfrac{x-12}{x-4}=\dfrac{-5x-10+x^2-11x+24}{\left(x-3\right)\left(x+2\right)}\)
=>\(\left(x-12\right)\left(x^2-x-6\right)=\left(x-4\right)\left(x^2-16x+14\right)\)
=>\(x^3-x^2-6x-12x^2+12x+72=x^3-16x^2+14x-4x^2+64x-56\)
=>\(-13x^2+6x+72=-20x^2+78x-56\)
=>\(7x^2-72x+128=0\)
=>\(\left[{}\begin{matrix}x=8\left(nhận\right)\\x=\dfrac{16}{7}\left(nhận\right)\end{matrix}\right.\)
c: ĐKXĐ: \(x\notin\left\{2;-2\right\}\)
\(\dfrac{x-1}{x+2}+\dfrac{2}{x-2}=\dfrac{12}{x^2-4}\)
=>\(\dfrac{x-1}{x+2}+\dfrac{2}{x-2}=\dfrac{12}{\left(x-2\right)\left(x+2\right)}\)
=>\(\dfrac{\left(x-1\right)\left(x-2\right)+2\left(x+2\right)}{\left(x+2\right)\left(x-2\right)}=\dfrac{12}{\left(x-2\right)\left(x+2\right)}\)
=>\(x^2-3x+2+2x+4=12\)
=>\(x^2-x-6=0\)
=>(x-3)(x+2)=0
=>\(\left[{}\begin{matrix}x=3\left(nhận\right)\\x=-2\left(loại\right)\end{matrix}\right.\)
NC
30 tháng 8 2020
Bài làm:
Δ ABC vuông tại A?
Ta có: \(\sin B=\frac{AC}{BC}=\frac{3}{5}\) <=> \(\frac{AC}{3}=\frac{BC}{5}=k\) \(\left(k\inℕ^∗\right)\)
=> \(AB^2=BC^2-CA^2=25k^2-9k^2=16k^2\)
=> \(AB=4k\)
Từ đây ta có thể dễ dàng tính được:
\(\cos B=\frac{AB}{BC}=\frac{4}{5}\) ; \(\tan B=\frac{AC}{AB}=\frac{3}{4}\) ; \(\cot B=\frac{AB}{AC}=\frac{4}{3}\)
30 tháng 8 2020
\(sin^2b+cos^2b=1\)
\(\left(\frac{3}{5}\right)^2+cos^2b=1\)
\(\frac{9}{25}+cos^2b=1\)
\(cos^2b=\frac{16}{25}\)
\(cosb=\pm\sqrt{\frac{16}{25}}=\pm\frac{4}{5}\)
\(tanb=\frac{sinb}{cosb}=\orbr{\begin{cases}\frac{\frac{3}{5}}{\frac{4}{5}}=\frac{3}{4}\\\frac{\frac{3}{5}}{\frac{-4}{5}}=\frac{-3}{4}\end{cases}}\)
\(cotb=\frac{1}{tanb}=\orbr{\begin{cases}\frac{1}{\frac{3}{4}}=\frac{4}{3}\\\frac{1}{\frac{-3}{4}}=\frac{-4}{3}\end{cases}}\)
25 tháng 9 2016
vì 1 phần mấy mà chả lớn hơn 0 9 / a+b+c =9a:2 b:2 c::2 nên a và b lớn hơn o k mình nha hứa rùi đó thực hiện 10 lần nhé
25 tháng 9 2016
xin lỗi nhưng em không biết,bởi vì em mới học lớp 6 thôi nên không biết gì cả.Nếu em bằng tuổi anh chị thì em đã giúp rồi nhưng em chưa học đến nên không biết.Thông cảm cho em.T T
PN
20 tháng 9 2017
Tokoyami bn đăng từng câu 1 thôi. Nhiều thế này thì ko đủ kiên nhẫn để làm đâu
20 tháng 9 2017
bạn này đang đau khổ
OoO_Nhok_Lạnh_Lùng_OoOhttps://olm.vn/thanhvien/hatho17 cái đứa này hack nik tớ
14 tháng 11 2016
\(A=2\sin^2\alpha+5\left(1-\sin^2\alpha\right)=5-3\sin^2\alpha=5-3\left(\frac{2}{3}\right)^2\)=\(\frac{11}{3}\)
HN
3 tháng 11 2016
bài này dùng hình vẽ để tính các cạnh tam giác vuoog đc ko nhỉ ?
7 tháng 9 2021
\(1,A=\left(\dfrac{\sqrt{x}}{\sqrt{x}-1}-\dfrac{1}{x-\sqrt{x}}\right):\left(\dfrac{1}{\sqrt{x}+1}+\dfrac{2}{x-1}\right)\left(x>0;x\ne1;x\right)\\ A=\dfrac{x-1}{\sqrt{x}\left(\sqrt{x}-1\right)}:\dfrac{\sqrt{x}-1+2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\\ A=\dfrac{\sqrt{x}+1}{\sqrt{x}}\cdot\left(\sqrt{x}-1\right)=\dfrac{x-1}{\sqrt{x}}\)
\(2,x=2\sqrt{2}+3=\left(\sqrt{2}+1\right)^2\\ \Leftrightarrow A=\dfrac{2\sqrt{2}+3}{\sqrt{2}+1}=\dfrac{\left(2\sqrt{2}+3\right)\left(\sqrt{2}-1\right)}{1}\\ =4\sqrt{2}-2\sqrt{2}+3\sqrt{2}-3=5\sqrt{2}-3\)