K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
T
3
1 tháng 6 2018
Cũng đang ôn thi sấp mặt luôn đây :)
Đưa được cái phương trình thôi còn lại bạn tự làm nha mai mình cũng thi rồi
\(\frac{90}{x}-1+\frac{3}{20}+\frac{90-x}{x+4}\)
Chúc thi tốt!!!!!!!!
25 tháng 11 2023
a: Sửa đề: A,B,M,O
Xét tứ giác BMOA có
\(\widehat{BMO}+\widehat{BAO}=90^0+90^0=180^0\)
=>BMOA là tứ giác nội tiếp
=>B,M,O,A cùng thuộc một đường tròn
b: Xét (O) có
BA,BM là tiếp tuyến
Do đó: BA=BM và OB là phân giác của \(\widehat{AOM}\)
=>\(\widehat{AOM}=2\cdot\widehat{AOB}\)
Xét (O) có
CA,CN là tiếp tuyến
Do đó: CA=CN và OC là phân giác của \(\widehat{AON}\)
=>\(\widehat{AON}=2\cdot\widehat{AOC}\)
\(\widehat{AON}+\widehat{AOM}=180^0\)(hai góc kề bù)
=>\(2\cdot\widehat{AOC}+2\cdot\widehat{AOB}=180^0\)
=>\(2\cdot\widehat{BOC}=180^0\)
=>\(\widehat{BOC}=90^0\)
Xét ΔOBC vuông tại O có OA là đường cao
nên \(OA^2=AB\cdot AC\)
mà AB=BM và AC=CN
nên \(OA^2=BM\cdot CN\)
c: BA=BM
=>B nằm trên đường trung trực của AM(1)
OA=OM
=>O nằm trên đường trung trực của AM(2)
Từ (1) và (2) suy ra BO là đường trung trực của AM
=>BO\(\perp\)AM tại trung điểm của AM
=>BO\(\perp\)AM tại H và H là trung điểm của AM
CA=CN
=>C nằm trên đường trung trực của AN(3)
OA=ON
=>O nằm trên đường trung trực của AN(4)
Từ (3) và (4) suy ra CO là đường trung trực của AN
=>CO\(\perp\)AN tại trung điểm của AN
=>CO\(\perp\)AN tại K và K là trung điểm của AN
Xét tứ giác AHOK có \(\widehat{AHO}=\widehat{AKO}=\widehat{HOK}=90^0\)
nên AHOK là hình chữ nhật
31 tháng 5 2016
a) Ta có : Góc SAB = 1/2 sđ cung AB ( Góc tạo bởi tiếp tuyến và dây cung)
Góc SCA = 1/2 sđ cung AB (Góc nội tiếp)
=> Góc SAB = Góc SCA
Xét hai tam giác : \(\Delta SAB\)và \(\Delta SCA\)có : Góc ASC chung , Góc SAB = góc SCA
=> \(\Delta SAB~\Delta SCA\left(g.g\right)\)\(\Rightarrow\frac{SA}{SC}=\frac{SB}{SA}\Rightarrow SA^2=SB.SC\)
b) Ta có SDA là góc ngoài của tam giác ACD \(\Rightarrow SDA=DAC+DCA=DAC+\frac{1}{2}sdAB\)
Mặt khác, ta có ; \(SAD=BAD+\frac{1}{2}sdAB=DAC+\frac{1}{2}sdAB\)( Vì AD là tia phân giác)
Do đó góc SDA = góc SAD => Tam giác SAD cân tại S => SA = SD
CM
4 tháng 5 2018
Đáp án C
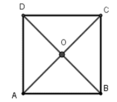
Gọi O là giao hai đường chéo của hình vuông ABCD.
Khi đó theo tính chất của hình vuông ta có OA = OB = OC = OD nên O là tâm đường tròn ngoại tiếp hình vuông ABCD, bán kính R = OA = AC/2
Xét tam giác vuông tại ta có:
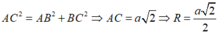
Vậy tâm đường tròn ngoại tiếp hình vuông ABCD cạnh a là giao điểm hai đường chéo, bán kính là R = a 2 2
CM
5 tháng 7 2017
Chọn đáp án C
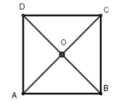
Gọi O là giao hai đường chéo của hình vuông ABCD.
Khi đó theo tính chất của hình vuông ta có OA = OB = OC = OD nên O là tâm đường tròn ngoại tiếp hình vuông ABCD, bán kính R = OA = AC/2
Xét tam giác vuông tại ta có:
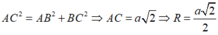
Vậy tâm đường tròn ngoại tiếp hình vuông ABCD cạnh a là giao điểm hai đường chéo, bán kính là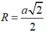 
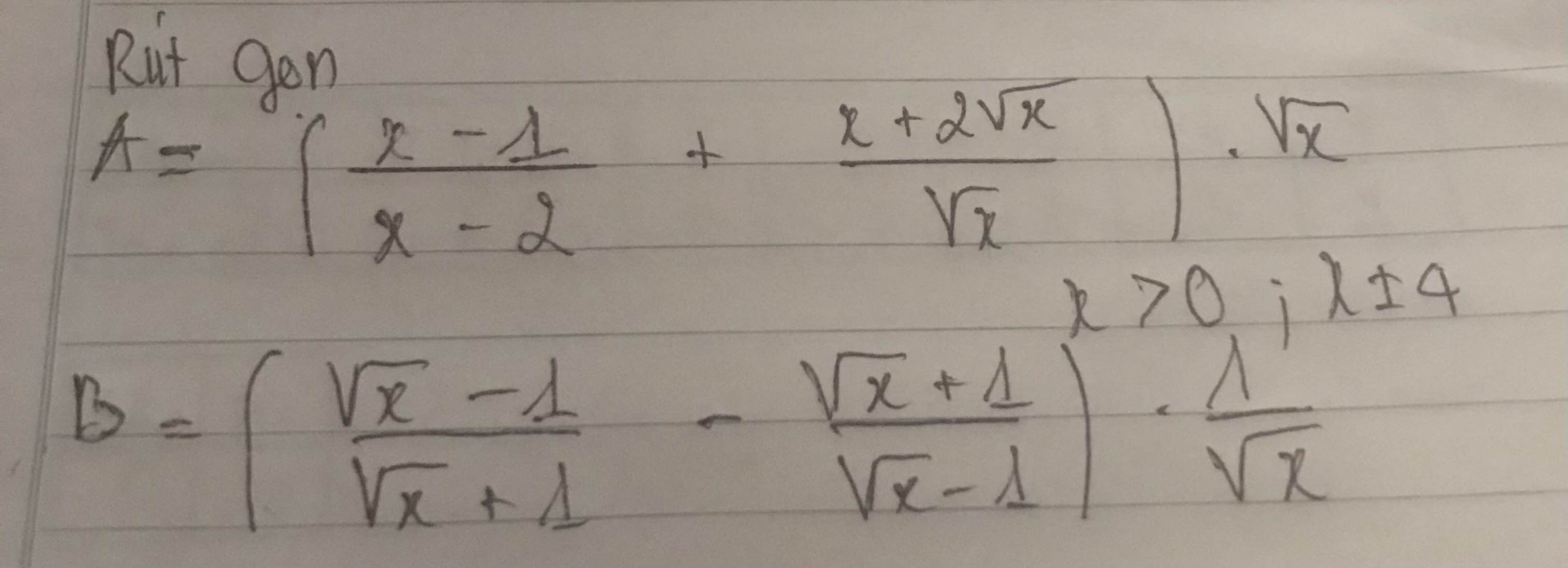
b: \(B=\dfrac{-4\sqrt{x}}{x-1}\cdot\dfrac{1}{\sqrt{x}}=\dfrac{-4}{x-1}\)
Làm ít tắt 1 tí thôi được không bạn