Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đồ thị hàm số f x = 2 x 3 + m x + 3 cắt trục hoành tại 3 điểm phân biệt có hoành độ a,b,c khi đó
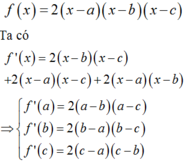
Khi đó ta có:
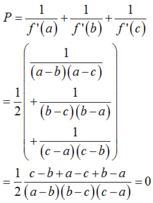
Chọn B.

Đáp án B
Đặt t = 2 sin x 2 ≥ t ≥ 0 dựa vào đường tròn lượng giác ta thấy:
Với t ∈ 0 ; 2 một giá trị của t có 6 giá trị của x
Với t = 2 một giá trị của t có 3 giá trị của x
Với t = 0 một giá trị của t có 4 giá trị của x
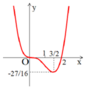
Dựa vào đồ thị ta thấy rằng PT f 2 sin x = f m có 12 nghiệm phân biệt ⇔ P T : f t = f m
có 2 nghiệm phân biệt thuộc khoảng 0 ; 2 ⇔ f m ∈ − 27 16 ; 0 ⇔ m ∈ 0 ; 2 ⇒ T = 4

Đáp án A
Đặt t = 2 x > 0 ⇒ t 2 − 2 m t + m + 2 = 0
ĐK PT có 2 nghiệm phân biệt là: Δ ' = m 2 − m − 2 > 0 S = 2 m > 0 P = m + 2 > 0 ⇔ m > 2
Khi đó: 2 x 1 = t 1 2 x 2 = t 2 ⇒ x 1 = log 2 t 1 ; x 2 = log 2 t 2
Để x 1 ; x 2 > 0 ⇔ t 1 > 1 ; t 2 > 1 ⇔ t 1 + t 2 > 2 t 1 − 1 t 2 − 1 > 0 ⇔ 2 m > 2 m + 2 − 2 m + 1 > 0 ⇔ 1 < m < 3
Vậy m ∈ 2 ; 3

Chọn đáp án A
Ta có
![]()
![]()
Đặt t = 2 x > 0 thì phương trình đã cho trở thành t 2 - 2 m . t + m + 2 = 0 *
Để phương trình đã cho có hai nghiệm dương phân biệt khi và chỉ khi phương trình (*) có hai nghiệm t 1 , t 2 lớn hơn 1.
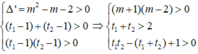
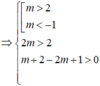
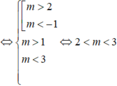
![]()





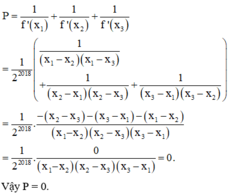

Hà Linh khôn thế