
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Hình 1: Qua O, kẻ tia OM nằm giữa hai tia OP và OQ sao cho OM//Pa//Qb
Ta có: OM//Pa
=>\(\hat{POM}+\hat{P}=180^0\) (hai góc trong cùng phía)
=>\(\hat{POM}=180^0-120^0=60^0\)
Ta có: OM//Qb
=>\(\hat{QOM}=\hat{Q}\) (hai góc trong cùng phía)
=>\(\hat{QOM}=30^0\)
Ta có: tia OM nằm giữa hai tia OP và OQ
=>\(\hat{POQ}=\hat{POM}+\hat{QOM}=60^0+30^0=90^0\)
=>\(x=90^0\)
Hình 2:
Qua O, kẻ tia OM nằm giữa hai tia OT và OQ sao cho OM//Qb//Pa
OM//Qb
=>\(\hat{MOQ}=\hat{OQb}\) (hai góc so le trong)
=>\(\hat{MOQ}=35^0\)
Ta có: tia OM nằm giữa hai tia OT và OQ
=>\(\hat{MOQ}+\hat{MOT}=\hat{TOQ}\)
=>\(\hat{MOT}=80^0-35^0=45^0\)
Qua T, kẻ tia Tm nằm giữa hai tia TO và TP sao cho Tm//Pa//OM
Ta có: Tm//Pa
=>\(\hat{mTP}=\hat{aPT}\) (hai góc so le trong)
=>\(\hat{mTP}=30^0\)
Ta có: Tm//OM
=>\(\hat{mTO}=\hat{TOM}\) (hai góc so le trong)
=>\(\hat{mTO}=45^0\)
Ta có: tia Tm nằm giữa hai tia TO và TP
=>\(\hat{OTP}=\hat{mTO}+\hat{mTP}=30^0+45^0=75^0\)
=>\(x=75^0\)

Hình 1: Qua O, kẻ tia OM nằm giữa hai tia OP và OQ sao cho OM//Pa//Qb
Ta có: OM//Pa
=>\(\hat{POM}+\hat{P}=180^0\) (hai góc trong cùng phía)
=>\(\hat{POM}=180^0-120^0=60^0\)
Ta có: OM//Qb
=>\(\hat{QOM}=\hat{Q}\) (hai góc trong cùng phía)
=>\(\hat{QOM}=30^0\)
Ta có: tia OM nằm giữa hai tia OP và OQ
=>\(\hat{POQ}=\hat{POM}+\hat{QOM}=60^0+30^0=90^0\)
=>\(x=90^0\)
Hình 2:
Qua O, kẻ tia OM nằm giữa hai tia OT và OQ sao cho OM//Qb//Pa
OM//Qb
=>\(\hat{MOQ}=\hat{OQb}\) (hai góc so le trong)
=>\(\hat{MOQ}=35^0\)
Ta có: tia OM nằm giữa hai tia OT và OQ
=>\(\hat{MOQ}+\hat{MOT}=\hat{TOQ}\)
=>\(\hat{MOT}=80^0-35^0=45^0\)
Qua T, kẻ tia Tm nằm giữa hai tia TO và TP sao cho Tm//Pa//OM
Ta có: Tm//Pa
=>\(\hat{mTP}=\hat{aPT}\) (hai góc so le trong)
=>\(\hat{mTP}=30^0\)
Ta có: Tm//OM
=>\(\hat{mTO}=\hat{TOM}\) (hai góc so le trong)
=>\(\hat{mTO}=45^0\)
Ta có: tia Tm nằm giữa hai tia TO và TP
=>\(\hat{OTP}=\hat{mTO}+\hat{mTP}=30^0+45^0=75^0\)
=>\(x=75^0\)



a,
\(C=\dfrac{1}{11}+\dfrac{1}{12}+\dfrac{1}{13}+...+\dfrac{1}{19}\\ C>0+0+0+...+0=0\left(1\right)\)
\(C=\dfrac{1}{11}+\dfrac{1}{12}+\dfrac{1}{13}+...+\dfrac{1}{19}\)
Ta có:
\(\dfrac{1}{11}< \dfrac{1}{10}\\ \dfrac{1}{12}< \dfrac{1}{10}\\ \dfrac{1}{13}< \dfrac{1}{10}\\ ...\\ \dfrac{1}{19}< \dfrac{1}{10}\)
\(\Rightarrow C< \dfrac{1}{10}+\dfrac{1}{10}+\dfrac{1}{10}+...+\dfrac{1}{10}\left(9\text{ phân số }\dfrac{1}{10}\right)\\ C< 9\cdot\dfrac{1}{10}\\ C< \dfrac{9}{10}< 1\left(2\right)\)
Từ (1) và (2) ta có:
\(0< C< 1\)
Rõ ràng \(0\) và \(1\) là hai số nguyên liên tiếp nên \(C\) không phải là số nguyên
Vậy \(C\) không phải là số nguyên (đpcm)
b,
\(D=2\left[\dfrac{1}{3}+\dfrac{1}{15}+\dfrac{1}{35}+...+\dfrac{1}{n\left(n+2\right)}\right]\\ D=\dfrac{2}{3}+\dfrac{2}{15}+\dfrac{2}{35}+...+\dfrac{2}{n\left(n+2\right)}\\ D>0+0+0+...+0=0\left(1\right)\)
Ta có:
\(D=\dfrac{2}{1\cdot3}+\dfrac{2}{3\cdot5}+\dfrac{2}{5\cdot7}+...+\dfrac{2}{n\cdot\left(n+2\right)}\\ D=\dfrac{1}{1}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{7}+...+\dfrac{1}{n}-\dfrac{1}{n+2}\\ D=\dfrac{1}{1}-\dfrac{1}{n+2}\\ D=1-\dfrac{1}{n+2}< 1\left(\text{Vì }n>0\right)\left(2\right)\)
Từ (1) và (2) ta có:
\(0< D< 1\)
Rõ ràng \(0\) và \(1\) là hai số nguyên liên tiếp nên \(D\) không phải là số nguyên
Vậy \(D\) không phải là số nguyên (đpcm)
c,
\(E=\dfrac{1}{3}+\dfrac{1}{4}+\dfrac{1}{5}+\dfrac{2}{7}+\dfrac{2}{9}+\dfrac{2}{11}\\ E=\dfrac{2}{6}+\dfrac{2}{8}+\dfrac{2}{10}+\dfrac{2}{7}+\dfrac{2}{9}+\dfrac{2}{11}\\ E=\dfrac{2}{6}+\dfrac{2}{7}+\dfrac{2}{8}+\dfrac{2}{9}+\dfrac{2}{10}+\dfrac{2}{11}\)
Ta có:
\(\dfrac{2}{6}>\dfrac{2}{12}\\ \dfrac{2}{7}>\dfrac{2}{12}\\ \dfrac{2}{8}>\dfrac{2}{12}\\ ...\\ \dfrac{2}{11}>\dfrac{2}{12}\)
\(\Rightarrow E>\dfrac{2}{12}+\dfrac{2}{12}+\dfrac{2}{12}+\dfrac{2}{12}+\dfrac{2}{12}+\dfrac{2}{12}\\ E>6\cdot\dfrac{2}{12}\\ E>\dfrac{12}{12}=1\left(1\right)\)
Mặt khác ta có:
\(\dfrac{2}{6}>\dfrac{2}{7}\\ \dfrac{2}{6}>\dfrac{2}{8}\\ \dfrac{2}{6}>\dfrac{2}{9}\\ ...\\ \dfrac{2}{6}>\dfrac{2}{11}\)
\(\Rightarrow E< \dfrac{2}{6}+\dfrac{2}{6}+\dfrac{2}{6}+\dfrac{2}{6}+\dfrac{2}{6}+\dfrac{2}{6}\\ E< 6\cdot\dfrac{2}{6}\\ E< 2\left(2\right)\)
Từ (1) và (2) ta có:
\(1< E< 2\)
Rõ ràng \(1\) và \(2\) là hai số nguyên liên tiếp nên \(E\) không phải là số nguyên
Vậy \(E\) không phải là số nguyên (đpcm)
c) \(E=\dfrac{1}{3}+\dfrac{1}{4}+\dfrac{1}{5}+\dfrac{2}{7}+\dfrac{2}{9}+\dfrac{2}{11}\)
\(=\dfrac{2}{6}+\dfrac{2}{8}+\dfrac{2}{10}+\dfrac{2}{7}+\dfrac{2}{9}+\dfrac{2}{11}\)
\(=2\left(\dfrac{1}{6}+\dfrac{1}{7}+\dfrac{1}{8}+\dfrac{1}{9}+\dfrac{1}{10}+\dfrac{1}{11}\right)\)
Ta có: \(\dfrac{1}{6}>\dfrac{1}{7}>\dfrac{1}{8}>\dfrac{1}{9}>\dfrac{1}{10}>\dfrac{1}{11}\)
\(\Rightarrow E>2\left(\dfrac{1}{11}+\dfrac{1}{11}+\dfrac{1}{11}+\dfrac{1}{11}+\dfrac{1}{11}+\dfrac{1}{11}\right)=2\left(\dfrac{1}{11}.6\right)=2\cdot\dfrac{6}{11}=\dfrac{12}{11}>1\) (1)
\(E< 2\left(\dfrac{1}{6}+\dfrac{1}{6}+\dfrac{1}{6}+\dfrac{1}{6}+\dfrac{1}{6}+\dfrac{1}{6}\right)=2\left(\dfrac{1}{6}.6\right)=2.1=2\) (2)
Từ (1) và (2) suy ra 1 < E < 2 suy ra E không phải là số nguyên


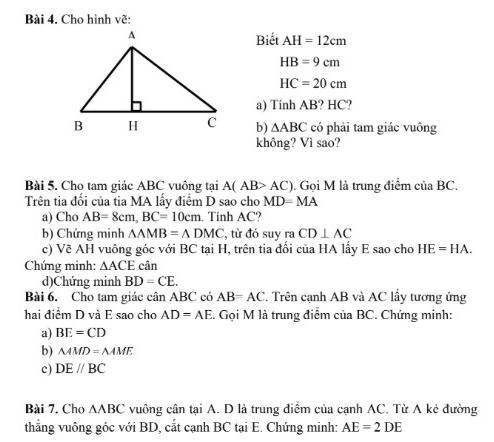
.jpg) Tính số đo góc P1. Nhớ làm rõ ra nha
Tính số đo góc P1. Nhớ làm rõ ra nha
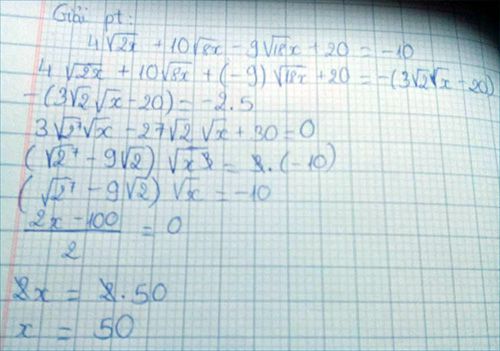



 helpppppp meeeeeeee !!!!!!!!!!!!!!!!!!
helpppppp meeeeeeee !!!!!!!!!!!!!!!!!!