LT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
DD
Cho \(a^2+\frac{1}{a^2}=7\).Tính \(a^3+\frac{1}{a^3}\), \(a^4+\frac{1}{a^4}\), \(a^5+\frac{1}{a^5}\)
1
25 tháng 6 2019
Ta có:
\(\left(a+\frac{1}{a}\right)^2=a^2+\frac{1}{a^2}+2=7+2=9\)
=> \(a+\frac{1}{a}=\pm3\)
+) Với \(a+\frac{1}{a}=3\)
Xét : \(\left(a+\frac{1}{a}\right)\left(a^2+\frac{1}{a^2}\right)=a^3+\frac{1}{a^3}+a+\frac{1}{a}\)
=> \(3.7=a^3+\frac{1}{a^3}+3\Leftrightarrow a^3+\frac{1}{a^3}=18\)
\(\left(a^2+\frac{1}{a^2}\right)\left(a^2+\frac{1}{a^2}\right)=a^4+\frac{1}{a^4}+2\)
\(\Rightarrow7.7=a^4+\frac{1}{a^4}+2\Rightarrow a^4+\frac{1}{a^4}=47\)
\(\left(a^4+\frac{1}{a^4}\right)\left(a+\frac{1}{a}\right)=a^5+\frac{1}{a^5}+a^3+\frac{1}{a^3}\)
=> \(47.3=a^5+\frac{1}{a^5}+18\Rightarrow a^5+\frac{1}{a^5}=123\)
Trường hợp còn lại em làm tương tự
2 tháng 2 2018
Có : a/ab+a+1 = a/ab+a+abc = 1/b+1+bc = 1/bc+b+1
c/ca+c+1 = bc/abc+bc+b = b/1+bc+b = b/bc+b+1
=> A = 1+bc+b/bc+b+1 = 1
Tk mk nha
KT
2 tháng 2 2018
BÀI 1:
\(\frac{a}{ab+a+1}+\frac{b}{bc+b+1}+\frac{c}{ca+c+1}\)
\(=\frac{a}{ab+a+1}+\frac{ab}{a\left(bc+b+1\right)}+\frac{abc}{ab\left(ca+c+1\right)}\)
\(=\frac{a}{ab+a+1}+\frac{ab}{abc+ab+a} +\frac{abc}{a^2bc+abc+ab}\)
\(=\frac{a}{ab+a+1}+\frac{ab}{ab+a+1}+\frac{1}{ab+a+1}\) (thay abc = 1)
\(=\frac{a+ab+1}{a+ab+1}=1\)
31 tháng 7 2020
1)
Ta có : \(\frac{a}{3}=\frac{b}{4}=\frac{c}{5}\)=> \(\frac{a^2}{9}=\frac{b^2}{16}=\frac{c^2}{25}\)=> \(\frac{a^2}{9}=\frac{2b^2}{32}=\frac{c^2}{25}\)
Đặt \(\frac{a^2}{9}=\frac{2b^2}{32}=\frac{c^2}{25}=k\)
=> \(\hept{\begin{cases}a^2=9k\\2b^2=32k\\c^2=25k\end{cases}}\)
=> \(a^2+2b^2-c^2=9k+32k-25k=16k\)
=> \(16k=144\)
=> \(k=9\)
Do đó \(\hept{\begin{cases}a^2=9\cdot9\\2b^2=32\cdot9\\c^2=25\cdot9\end{cases}}\Rightarrow\hept{\begin{cases}a^2=81\\b^2=144\\c^2=225\end{cases}}\Rightarrow\hept{\begin{cases}a=9\\b=12\\c=15\end{cases}}\)
2) Ta có : \(\frac{a}{5}=\frac{b}{7}=\frac{c}{9}\)=> \(\frac{a^2}{25}=\frac{b^2}{49}=\frac{c^2}{81}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có :
\(\frac{a^2}{25}=\frac{b^2}{49}=\frac{c^2}{81}=\frac{a^2+b^2-c^2}{25+49-81}=\frac{-28}{-7}=4\)
=> \(\hept{\begin{cases}\frac{a^2}{25}=4\\\frac{b^2}{49}=4\\\frac{c^2}{81}=4\end{cases}}\Rightarrow\hept{\begin{cases}a^2=100\\b^2=196\\c^2=324\end{cases}}\Rightarrow\hept{\begin{cases}a=10\\b=14\\c=18\end{cases}}\)
TT
31 tháng 7 2020
a) đặt \(\frac{a}{3}=\frac{b}{4}=\frac{c}{5}=k\Rightarrow\hept{\begin{cases}a=3k\\b=4k\\c=5k\end{cases}}\)
đặt \(a^2+2b^2-c^2=144\)
\(\Leftrightarrow\left(3k\right)^2+2\left(4k\right)^2-\left(5k\right)^2=144\)
\(\Leftrightarrow9k^2+32k^2-25k^2=144\)
\(\Leftrightarrow k^2\left(9+32-25\right)=144\)
\(\Leftrightarrow k^216=144\)
\(\Leftrightarrow k^2=9\)
\(\Leftrightarrow k=\sqrt{9}=\pm3\)
do đó
\(\frac{a}{3}=k\Leftrightarrow\frac{a}{3}=\pm3\Rightarrow\hept{\begin{cases}a=3.3=9\\a=3.\left(-3\right)=-9\end{cases}}\)
\(\frac{b}{4}=k\Leftrightarrow\frac{b}{4}=\pm3\Rightarrow\hept{\begin{cases}b=4.3=12\\b=4.\left(-3\right)=-12\end{cases}}\)
\(\frac{c}{5}=k\Leftrightarrow\frac{c}{5}=\pm3\Rightarrow\hept{\begin{cases}c=5.3=15\\c=5.\left(-3\right)=-15\end{cases}}\)
vậy các cặp a,b,c thỏa mãn là \(\left\{a=9;b=12;c=15\right\}\left\{a=-9;b=-12;c=-15\right\}\)
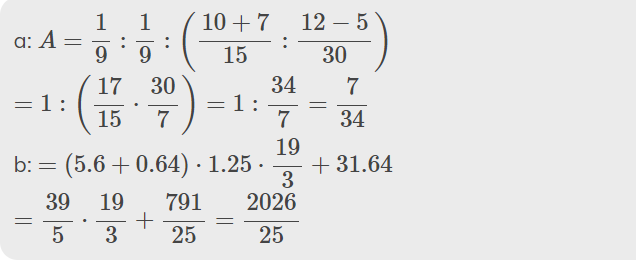
đề là sao bn