Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(T=\dfrac{3}{5\cdot7}+\dfrac{3}{7\cdot9}+\dfrac{3}{9\cdot11}+...+\dfrac{3}{59\cdot61}\)
\(=\dfrac{3}{2}\cdot\left(\dfrac{2}{5\cdot7}+\dfrac{2}{7\cdot9}+\dfrac{2}{9\cdot11}+...+\dfrac{2}{59\cdot61}\right)\)
\(=\dfrac{3}{2}\cdot\left(\dfrac{1}{5}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{9}+...+\dfrac{1}{59}-\dfrac{1}{61}\right)\)
\(=\dfrac{3}{2}\cdot\left(\dfrac{1}{5}-\dfrac{1}{61}\right)=\dfrac{3}{2}\cdot\dfrac{56}{305}=\dfrac{84}{305}\)
\(\dfrac{3}{5.7}+\dfrac{3}{7.9}+\dfrac{3}{9.11}+...+\dfrac{3}{59.61}\)
\(=3.\left(\dfrac{1}{5.7}+\dfrac{1}{7.9}+\dfrac{1}{9.11}+...+\dfrac{1}{59.61}\right)\)
\(=3.\dfrac{1}{2}.\left(\dfrac{1}{5}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{9}+....+\dfrac{1}{59}-\dfrac{1}{61}\right)\)
\(=\dfrac{3}{2}.\left(\dfrac{1}{5}-\dfrac{1}{61}\right)\)
\(=\dfrac{3}{2}.\dfrac{56}{305}\)
\(=\dfrac{84}{305}\)

\(\dfrac{3}{5.7}+\dfrac{3}{7.9}+...+\dfrac{3}{59.61}\)
= \(\dfrac{2}{2}.\left(\dfrac{3}{5.7}+\dfrac{3}{7.9}+...+\dfrac{3}{59.61}\right)\)
= \(\dfrac{3}{2}.\left(\dfrac{2}{5.7}+\dfrac{2}{7.9}+...+\dfrac{2}{59.61}\right)\)
= \(\dfrac{3}{2}.\left(\dfrac{1}{5}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{9}+...+\dfrac{1}{59}-\dfrac{1}{61}\right)\)
= \(\dfrac{3}{2}.\left(\dfrac{1}{5}-\dfrac{1}{61}\right)\)
=\(\dfrac{3}{2}.\dfrac{56}{305}\)
= \(\dfrac{78}{305}\)
\(\left(x^2-4\right)\left(6-2x\right)=0\) ⇔ \(x^2-4=0\) hoặc \(6-2x=0\)
*Nếu \(x^2-4=0\)
⇒ x2 = 4
⇒ x ∈ {2 ; -2}
*Nếu \(6-2x=0\)
⇒2x = 6
⇒ x = 6 : 2 = 3
Vậy x ∈ { -2 ; 2 ; 3 }

a) Sửa tí: \(1+\dfrac{1}{2}+\dfrac{1}{2^2}+\dfrac{1}{2^3}+...+\dfrac{1}{2^{2006}}\)
Đặt \(A=1+\dfrac{1}{2}+\dfrac{1}{2^2}+\dfrac{1}{2^3}+...+\dfrac{1}{2^{2006}}\)
\(\Rightarrow2A=2.\left(1+\dfrac{1}{2}+\dfrac{1}{2^2}+\dfrac{1}{2^3}+...+\dfrac{1}{2^{2006}}\right)\)
\(\Rightarrow2A=2+1+\dfrac{1}{2}+\dfrac{1}{2^2}+...+\dfrac{1}{2^{2005}}\)
\(\Rightarrow2A-A=2+1+\dfrac{1}{2}+\dfrac{1}{2^2}+...+\dfrac{1}{2^{2005}}-\left(1+\dfrac{1}{2}+\dfrac{1}{2^2}+...+\dfrac{1}{2^{2006}}\right)\)
\(\Rightarrow A=2+1+\dfrac{1}{2}+\dfrac{1}{2^2}+...+\dfrac{1}{2^{2005}}-1-\dfrac{1}{2}-\dfrac{1}{2^2}-\dfrac{1}{2^3}-...-\dfrac{1}{2^{2006}}\)
\(\Rightarrow A=2-\dfrac{1}{2^{2006}}\)
b) Đặt \(A=\dfrac{2}{5.7}+\dfrac{2}{7.9}+\dfrac{2}{9.11}+...+\dfrac{1}{50.61}\)
\(A=\dfrac{1}{5}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{9}+\dfrac{1}{9}-...+\dfrac{1}{59}-\dfrac{1}{61}\)
\(A=\dfrac{1}{5}-\dfrac{1}{61}\)
\(A=\dfrac{56}{305}\)
c) Đặt \(A=\dfrac{7}{3}+\dfrac{7}{15}+\dfrac{7}{35}+...+\dfrac{7}{9999}\)
\(A=\dfrac{7}{2}.2.\left(\dfrac{1}{3}+\dfrac{1}{5}+...+\dfrac{1}{9999}\right)\)
\(A=\dfrac{7}{2}.\left(1-\dfrac{1}{101}\right)\)
\(A=\dfrac{7}{2}.\dfrac{100}{101}\)
\(A=\dfrac{256}{101}\)

Theo quy luật thì mình nghĩ đáng lẽ \(\dfrac{4}{5.9}\)phải là\(\dfrac{4}{7.9}\)Bạn có chép sai đề ko?
A=1-\(\dfrac{4}{5.7}-\dfrac{4}{7.9}-\dfrac{4}{9.11}...-\dfrac{4}{59.61}\)
A=\(1-\left(\dfrac{4}{5.7}+\dfrac{4}{7.9}+\dfrac{4}{9.11}+...+\dfrac{4}{59.61}\right)\)
Đặt B=\(\dfrac{4}{5.7}+\dfrac{4}{7.9}+\dfrac{4}{9.11}+...+\dfrac{4}{59.61}\)

. Ta có :
\(\dfrac{1}{11}>\dfrac{1}{20}\)
\(\dfrac{1}{12}>\dfrac{1}{20}\)
.................
\(\dfrac{1}{19}>\dfrac{1}{20}\)
\(\dfrac{1}{20}=\dfrac{1}{20}\)
\(\Leftrightarrow\dfrac{1}{11}+\dfrac{1}{12}+......+\dfrac{1}{20}>\dfrac{1}{20}+\dfrac{1}{20}+.....+\dfrac{1}{20}\)
\(\Leftrightarrow S>\dfrac{1}{20}.10\)
\(\Leftrightarrow S>\dfrac{1}{2}\)
2. \(\dfrac{x}{12}=\dfrac{-1}{24}-\dfrac{1}{8}\)
\(\Leftrightarrow\dfrac{x}{12}=-\dfrac{1}{6}\)
\(\Leftrightarrow6x=-12\)
\(\Leftrightarrow x=-2\)
Vậy ...
3. \(\dfrac{2}{5.7}+\dfrac{2}{7.9}+........+\dfrac{2}{19.21}\)
\(=\dfrac{1}{5}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{9}+......+\dfrac{1}{19}-\dfrac{1}{21}\)
\(=\dfrac{1}{5}-\dfrac{1}{21}\)
\(=\dfrac{16}{105}\)

Ta có :
\(A=\dfrac{4}{5.7}+\dfrac{4}{7.9}+............+\dfrac{4}{59.61}\)
\(\dfrac{A}{2}=\dfrac{2}{5.7}+\dfrac{2}{7.9}+..............+\dfrac{2}{59.61}\)
\(\dfrac{A}{2}=\dfrac{1}{5}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{9}+.......+\dfrac{1}{59}-\dfrac{1}{61}\)
\(\dfrac{A}{2}=\dfrac{1}{5}-\dfrac{1}{61}\)
\(\dfrac{A}{2}=\dfrac{56}{305}\)
\(\Rightarrow A=\dfrac{112}{305}\)
Chúc bn học tốt!!
\(A=\dfrac{4}{5.7}+\dfrac{4}{7.9}+...+\dfrac{4}{59.61}\)
\(A=2\left(\dfrac{2}{5.7}+\dfrac{2}{7.9}+...+\dfrac{2}{59.61}\right)\)
\(A=2\left(\dfrac{1}{5}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{9}+...+\dfrac{1}{59}-\dfrac{1}{61}\right)\)
\(A=2\left(\dfrac{1}{5}-\dfrac{1}{61}\right)\)
\(A=2.\dfrac{56}{305}\)
\(A=\dfrac{112}{305}\)

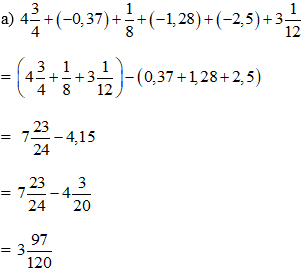
Em nhớ nhân 1/2 trong tất cả dấu bằng thì biểu thức này mới không thay đổi kết quả nhé.
`11/(5.7) + 11/(7.9) + 11/(9.11) + ... + 11/(59.61)`
`= 2.(11/(5.7) + 11/(7.9) + ... + 11/(59.61))`
`= 11.(2/(5.7) + 2/(7.9) + ... + 2/(59.61))`
`= 11.(1/5 - 1/7 + 1/7 - 1/9 + ... +1/59 - 1/61)`
`= 11.(1/5 - 1/61)`
`= 11.56/305`
`= 616/305`