Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)biến đổi vế trái ta đc:x(y+z)-y(x-z)=xy+xz-xy+yz
=(xz+yz)+(xy-xy)
=z(x+y)=vế phải(đpcm)
b)biến đổi vế trái ta đc:x(y-z)-x(y+a)=xy-xz-xy-xa
=(xy-xy)-(xz+xa)
=-(xz+xa)
=-x(z+a)=vế phải(đpcm)
a;\(x\left(y+z\right)-y\left(x-z\right)=\left(x+y\right)z\)
\(xy+xz-xy+yz=\left(x+y\right)z\)
\(xz+yz=\left(x+y\right)z\)
\(\left(x+y\right)z=\left(x+y\right)z\left(ĐPCM\right)\)
b;\(x\left(y-z\right)-x\left(y+a\right)=-x\left(z+a\right)\)
\(xy-xz-xy-xa=-x\left(z+a\right)\)
\(-xz-xa=-x\left(z+a\right)\)
\(-x\left(z+a\right)=-x\left(z+a\right)\left(ĐPCM\right)\)
P/S: sai thì thôi nha

Bài 1:
a: \(\Leftrightarrow\left(x-2\right)^2=25\)
=>x-2=5 hoặc x-2=-5
=>x=7 hoặc x=-3
b: \(\Leftrightarrow6x+24-5x-2=0\)
=>x+22=0
hay x=-22
c: \(\Leftrightarrow35-15x+14+14x=0\)
=>49-x=0
hay x=49

a/ \(\left(-4\right)\left(x-2\right)^2=-100\)
\(\Leftrightarrow\left(x-2\right)^2=\left(-100\right):\left(-4\right)\)
\(\Leftrightarrow\left(x-2\right)^2=25\)
\(\Leftrightarrow\left[{}\begin{matrix}x-2=5\\x-2=-5\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=7\\x=-3\end{matrix}\right.\)
Vậy ...
b/ \(3\left(2x+8\right)-\left(5x+2\right)=0\)
\(\Leftrightarrow6x+24=5x+2\)
\(\Leftrightarrow6x-5x=2-24\)
\(\Leftrightarrow x=-22\)
Vậy ....
c/ \(5\left(7-3x\right)+7\left(2+2x\right)=0\)
\(\Leftrightarrow5\left(7-3x\right)=-7\left(2+2x\right)\)
\(\Leftrightarrow35-15x=-14+\left(-14\right)x\)
\(\Leftrightarrow35+14=\left(-14\right)x+15x\)
\(\Leftrightarrow x=49\)
Vậy ....

a. Biểu thức không viết được thành tích. Bạn xem lại.
b. $(x-y)a+(x+y)b+(y+z)a+(z-y)b$
$=a(x-y+y+z)+b(x+y+z-y)$
$=a(x+z)+b(x+z)=(x+z)(a+b)$
c. $(x-y)a+(x+y)b+(y+z)a+(z-y)b$
$=a(x-y+y+z)+b(x+y+z-y)=a(x+z)+b(x+z)=(x+z)(a+b)$
d. $(x+y+z)a+(-x-y-z)a+a(x+y)+az$
$=(x+y+z)a-(x+y+z)a+a(x+y+z)=a(x+y+z)$

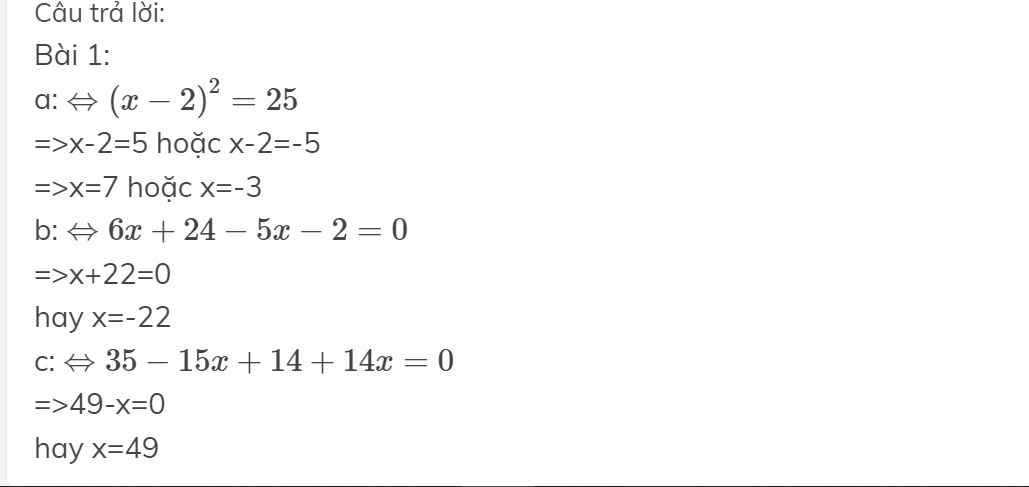
Bài 2:
a: \(=xy+xz-xy+yz\)
\(=xz+yz=z\left(x+y\right)\)
b: \(=x\left(y-z-y-a\right)\)
\(=x\left(-z-a\right)=-x\left(z+a\right)\)
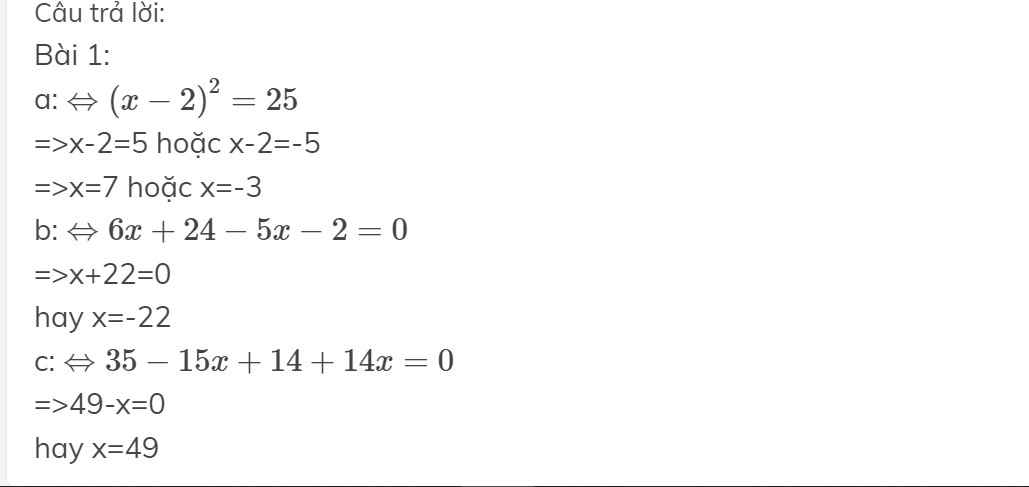
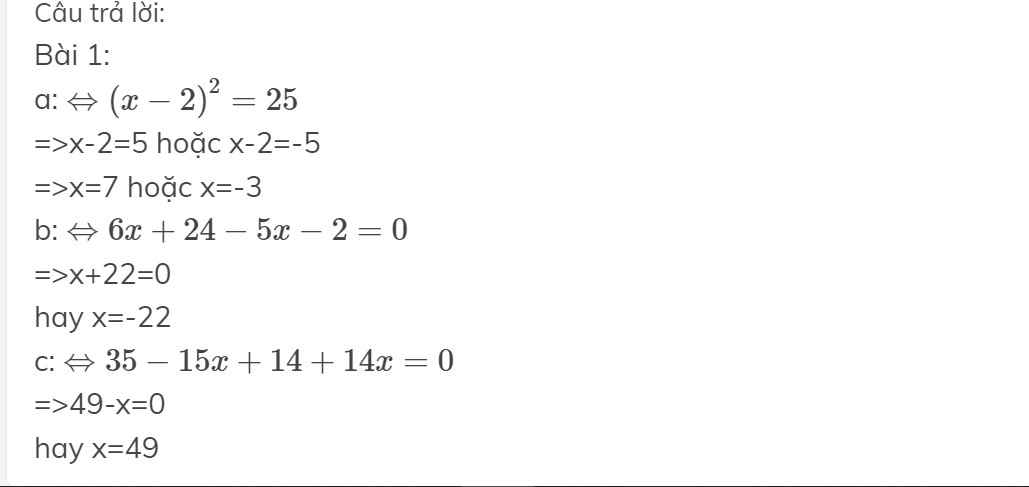

a) \(\left(x-y\right)-\left(x-z\right)=\left(z+x\right)-\left(y+x\right)\)
BL:
Ta có: \(\left(x-y\right)-\left(x-z\right)\)
\(=x-y-x+z\)
\(=z+x-y-x\)
\(=\left(z+x\right)-\left(y+x\right)\)
\(\Rightarrow\) \(\left(x-y\right)-\left(x-z\right)=\left(z+x\right)-\left(y+x\right)\)
b) \(\left(x-y+z\right)-\left(y+z-x\right)-\left(x-y\right)=\left(z-y\right)-\left(z-x\right)\)
BL:
Lại có: \(\left(x-y+z\right)-\left(y+z-x\right)-\left(x-y\right)\)
\(=x-y+z-y-z+x-x+y\)
\(=\left(x-y-x+y\right)+\left(z-y\right)-\left(z-x\right)\)
\(=\left(z-y\right)-\left(z-x\right)\)
\(\Rightarrow\) \(\left(x-y+z\right)-\left(y+z-x\right)-\left(x-y\right)=\left(z-y\right)-\left(z-x\right)\)