K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
20 tháng 10 2017
\(\overline{1abc}=9\overline{abc}\)
\(\Rightarrow1000+\overline{abc}=9\overline{abc}\)
\(\Rightarrow1000=8\overline{abc}\)
\(\Rightarrow\overline{abc}=125\)
NV
Nguyễn Việt Lâm
Giáo viên
1 tháng 6 2020
Đường cao xuất phát từ đỉnh nào? Đỉnh A?
\(\overrightarrow{BC}=\left(4;-6\right)=2\left(2;-3\right)\)
Pt BC: \(3\left(x-1\right)+2\left(y+2\right)=0\Leftrightarrow3x+2y+1=0\)
Gọi AH là đường cao xuất phát từ A \(\Rightarrow AH\perp BC\)
\(\Rightarrow\) Đường thẳng AH nhận \(\left(2;-3\right)\) là 1 vtpt
Phương trình AH: \(2\left(x-3\right)-3\left(y+1\right)=0\Leftrightarrow2x-3y-9=0\)
H là giao điểm AH và BC nên tọa độ là nghiệm:
\(\left\{{}\begin{matrix}3x+2y+1=0\\2x-3y-9=0\end{matrix}\right.\) \(\Rightarrow H\left(\frac{15}{13};-\frac{29}{13}\right)\)
2.
Gọi I là trung điểm EF \(\Rightarrow I\left(1;1\right)\)
\(\overrightarrow{EF}=\left(2;-4\right)=2\left(1;-2\right)\)
Trung trực EF vuông góc EF và qua I nên có pt:
\(1\left(x-1\right)-2\left(y-1\right)=0\Leftrightarrow x-2y+1=0\)
M là giao điểm d và trung trực EF nên tọa độ là nghiệm:
\(\left\{{}\begin{matrix}x-2y+1=0\\x-y+2=0\end{matrix}\right.\) \(\Rightarrow M\left(-3;-1\right)\)
A
2 tháng 7 2019
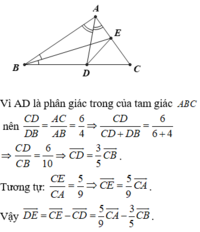
Gọi ( O;R ) , ( I ;r ) lần lượt là các đường tròn ngoại tiếp tam giác ABC, DEF
Tam giác ABC ~ Tam giác DEF ( vì \(\widehat{ABC}=\widehat{DEF};\widehat{BAC}=\widehat{EDF}\)) \(\Rightarrow\widehat{ABC}=\widehat{DEF}\)
\(\widehat{ACB},\widehat{DEF}\)nhọn nên \(\widehat{ACB}=\frac{1}{2}\widehat{AOB};\widehat{DEF}=\frac{1}{2}\widehat{DIE}\)( hệ quả góc nội tiếp )
\(\Rightarrow\widehat{AOB}=\widehat{DIE}\)
\(OA=OB\left(=R\right)\Rightarrow\Delta OAB\)cân tại O
\(ID=IE\left(=r\right)\Rightarrow\Delta IDE\)cân tại I
Do đó Tam giác OAB ~ Tam giác IDE \(\Rightarrow\frac{OA}{ID}=\frac{AB}{DE}\Rightarrow\frac{R}{r}=\frac{3DE}{DE}\)
\(\Rightarrow R=3r\) ( đpcm)
5 tháng 7 2019
Gọi ( O; R ), ( I; R ) lần lượt là các đường tròn ngoại tiếp tam giác ABC, DEF
Tam giác ABC ~ Tam giác DEF ( vì \(\widehat{ABC}=\widehat{DEF;}\widehat{BAC}=\widehat{EDF}\) ) \(\Rightarrow\widehat{ABC}=\widehat{DEF}\)
\(\widehat{ABC}=\widehat{DEF}\)nhọn nên \(\widehat{ACB}=\frac{1}{2}\widehat{AOB};\widehat{DEF}=\frac{1}{2}\widehat{DIE}\)(hệ quả góc nội tiếp )
\(\Rightarrow\widehat{AOB}=\widehat{DIE}\)
\(OA=OA\left(=R\right)\Rightarrow\Delta OAB\)cân tại O
Do đó Tam giác OAB ~ Tam giác IDE\(\Rightarrow\frac{OA}{ID}=\frac{AB}{DE}\Rightarrow\frac{R}{r}=\frac{3DE}{DE}\)
\(\Rightarrow R=3r\left(đpcm\right)\)
Rất vui vì giúp đc bạn <3
30 tháng 5 2022
a: Xét ΔABC vuông tại A và ΔADE vuông tại A có
AB/AD=AC/AE
Do đó: ΔABC\(\sim\)ΔADE
b: \(BC=\sqrt{24^2+32^2}=40\)
\(DE=\sqrt{9^2+12^2}=15\)
c: Ta có: ΔABC\(\sim\)ΔADE
nên \(\widehat{ABC}=\widehat{ADE}\)
mà hai góc này ở vị trí so le trong
nên BC//DE
LC
1
NV
Nguyễn Việt Lâm
Giáo viên
14 tháng 9 2020
\(\overrightarrow{AD}=\overrightarrow{GC}\Rightarrow ADCG\) là hbh \(\Rightarrow\overrightarrow{CD}=\overrightarrow{GA}\)
Tương tự DEBG là hbh \(\Rightarrow\overrightarrow{DE}=\overrightarrow{GB}\)
\(\overrightarrow{GE}=\overrightarrow{GC}+\overrightarrow{CD}+\overrightarrow{DE}=\overrightarrow{GC}+\overrightarrow{GA}+\overrightarrow{GB}=\overrightarrow{0}\)