
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



xin lỗi nha mình không biết chủ đề nào nên mới chọn đại đây là bài của lớp 7 nha các bạn

\(2^x=x^2\Rightarrow xln2=2lnx\Rightarrow\frac{ln2}{2}=\frac{lnx}{x}\Rightarrow x=2\)
Ta cũng có \(\frac{2ln2}{2.2}=\frac{lnx}{x}\Rightarrow\frac{ln4}{4}=\frac{lnx}{x}\Rightarrow x=4\) \(\Rightarrow\left\{{}\begin{matrix}a=2\\b=4\end{matrix}\right.\)
Pt dưới: \(4logx-\frac{logx}{loge}=log4\)
\(\Leftrightarrow logx\left(4-ln10\right)=log4\Leftrightarrow logx\left(ln\left(\frac{e^4}{10}\right)\right)=log4\)
\(\Rightarrow logx=\frac{log4}{ln\left(\frac{e^4}{10}\right)}=log4.log_{\frac{e^4}{10}}e\)
\(\Rightarrow x=10^{log4.log_{\frac{e^4}{10}}e}=\left(10^{log4}\right)^{log_{\frac{e^4}{10}}e}=2^{2.log_{\frac{e^4}{10}}e}\)
\(\Rightarrow\left\{{}\begin{matrix}c=2\\d=4\end{matrix}\right.\)
Bạn tự thay kết quả và tính

ta gọi số cần tìm có dạng abcd và tổng các chữ số là (a+b+c+d). ĐK: a,b,c,d thuộc (0;10)
vì 0<(a+b+c+d)<40
<=> 2359 - 0 < 2359 - (a+b+c+d) < 2359 - 4
mặt khác, vì abcd + (a+b+c+d) = 2359 => abcd = 2359 - (a+b+c+d)
thay vào, ta có:
2359 > abcd > 2319
số abcd nằm trong khoảng (2319->2359) => số đó phải có dạng 23xy => a=2,b=3, cd thuộc khoảng (19->59)
mà ta có abcd + (a+b+c+d) = 2359
<=> 2300 + cd + (2+3+c+d) = 2359
<=> 11c + 2d = 54
<=> d = (54-11c)/2
để d là số tự nhiên => (54-11c) phải là số chẵn => c phải chẵn
c= 0 => d=54/2 = 27 (>9) => loại
c= 2 => d= 32/2 = 16 (>9) => loại
c= 4 => d= 10/2 = 5
=> số cần tìm abcd chính là 2345


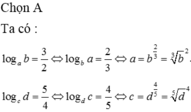

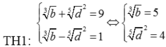
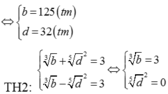
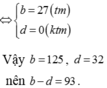
a + b + c + d + a + b + c + d = 2( d + c + b + a)