Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

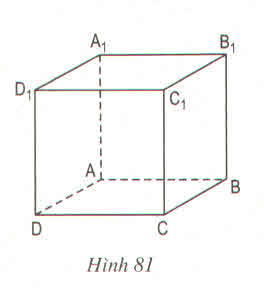
Với hình hộp chữ nhật ABCD. A 1B1C1D1
a) Nếu O là trung điểm của đoạn CB1 thì O cũng là trung điểm của đoạn C1B vì CBB1C1 là hình chữ nhật nên hai đường chéo có chung một trung điểm.
b) K là điểm thuộc cạnh CD thì K không thuộc cạnh BB1 vì bốn điểm C, D, B, B1 không thuộc một mặt phẳng

) Những cạnh song song với cạnh CC1 là: AA1, BB1, DD1
b) Những cạnh song song với cạnh A1D1 là: B1C1, BC, AD

a. Ta có: AD // BC, đường thẳng AD1 cắt AD nhưng nó không cắt BC.
Vậy mệnh đề a sai.
b. Hai đường thẳng AA1 và BC không có điểm chung nhưng chúng không song song
Vậy mệnh đề b sai.

a. Ta có: A1B1 // mp(ABCD)
A1B1 // mp(CDD1C1)
b. Ta có: AC // A1C1
Suy ra: AC không thuộc mp(A1B1C1)

Ta có AD vuông góc với D1D vì A1D1DA là hình chữ nhật
Tương tự => DC cũng vuông góc với D1D
Mà AD chỉ vuông góc với DC vì ABCD là hình chữ nhật mà thôi chứ không song song
=> Mệnh đề trên là sai
(>Tích đúng cho mình nha<) ![]()

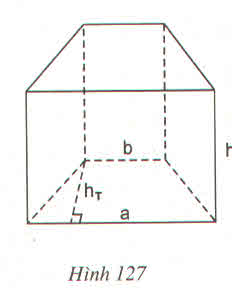
diện tích xung quanh của lăng trụ là (\(\sqrt{53}\times2+11+15)\)\(\times\)14\(\approx\)567,8mm2
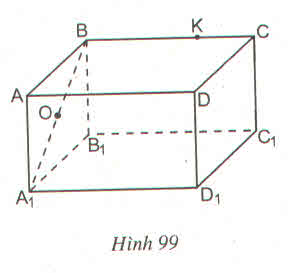
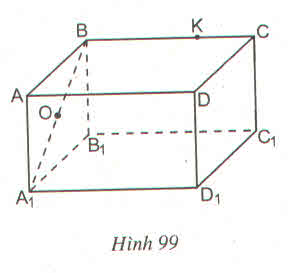

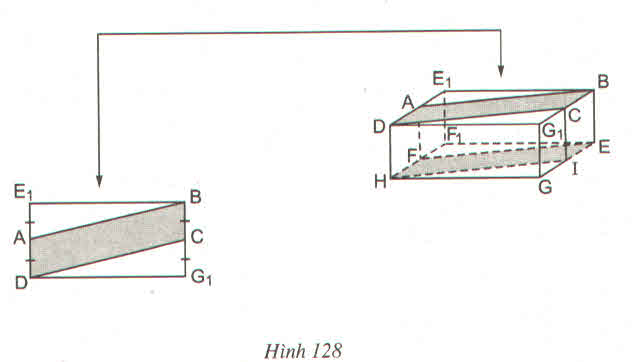
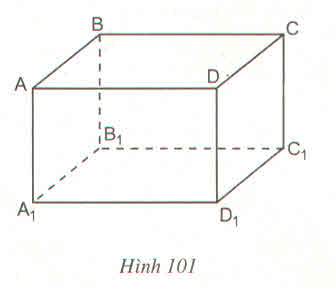



a) Câu trả lời trên là có. Thật vậy, vì mặt bên BCC1B1 là hình chữ nhật có O là trung điểm của đường chéo CB1 nên O cũng là trung điểm của đường chéo BC1 (theo tính chất đường chéo của hình chữ nhật). Vậy thuộc đoạn BC1.
b) K không thuộc cạnh BB1 vì K ∉ mp( BB1C1C ) mà BB1 thuộc mặt phẳng đó
Vậy K không thuộc cạnh BB1.