Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Gọi q là công sai của cấp số nhân. Ta có: \(a;b=aq;c=aq^2\).
\(a^2b^2c^2\left(\dfrac{1}{a^3}+\dfrac{1}{b^3}+\dfrac{1}{c^3}\right)=\dfrac{b^2c^2}{a}+\dfrac{a^2c^2}{b}+\dfrac{a^2b^2}{c}\)
\(=\dfrac{\left(a.q\right)^2\left(a.q^2\right)^2}{a}+\dfrac{a^2\left(aq^2\right)^2}{aq}+\dfrac{a^2\left(aq\right)^2}{aq^2}\)
\(=\dfrac{a^2q^2a^2q^4}{a}+\dfrac{a^2a^2q^4}{aq}+\dfrac{a^2a^2q^2}{aq^2}\)
\(=a^3q^6+a^3q^3+a^3\)
\(=\left(a^2q\right)^3+\left(aq\right)^3+a^3\)
\(=c^3+b^3+a^3=a^3+b^3+c^3\).
b) Gọi q là công bội của của cấp số nhân.
Ta có: \(a;b=aq;c=aq^2;d=aq^3\).
\(\left(ab+bc+cd\right)^2=\left(a.aq+aq.aq^2+aq^2.aq^3\right)^2\)
\(=\left(a^2q+a^2q^3+a^2q^5\right)^2=a^4q^2\left(1+q^2+q^4\right)^2\). (1)
\(\left(a^2+b^2+c^2\right)\left(b^2+c^2+d^2\right)\)\(=\left(a^2+a^2q^2+a^2q^4\right)\left(a^2q^2+a^2q^4+a^2q^6\right)\)
\(=a^2\left(1+q^2+q^4\right)a^2q^2\left(1+q^2+q^4\right)\)
\(=a^4q^2\left(1+q^2+q^4\right)^2\). (2)
So sánh (1) và (2) ta có điều phải chứng minh.

1: \(Q=\dfrac{ab\left(a-b\right)}{ab}\cdot\dfrac{\sqrt{a}+\sqrt{b}}{\sqrt{a}-\sqrt{b}}=\left(\sqrt{a}+\sqrt{b}\right)^2=a+2\sqrt{ab}+b\)
2: \(=\dfrac{-1+\sqrt{5}-\sqrt{5}+\sqrt{9}-...-\sqrt{2001}+\sqrt{2005}}{4}\)
\(=\dfrac{\sqrt{2005}-1}{4}\)

a) Đặt t = cos![]() , t ∈ [-1 ; 1] thì phương trình trở thành
, t ∈ [-1 ; 1] thì phương trình trở thành
(1 - t2) - 2t + 2 = 0 ⇔ t2 + 2t -3 = 0 ⇔ ![]()
Phương trình đã cho tương đương với
cos![]() = 1 ⇔
= 1 ⇔ ![]() = k2π ⇔ x = 4kπ, k ∈ Z.
= k2π ⇔ x = 4kπ, k ∈ Z.
b) Đặt t = sinx, t ∈ [-1 ; 1] thì phương trình trở thành
8(1 - t2) + 2t - 7 = 0 ⇔ 8t2 - 2t - 1 = 0 ⇔ t ∈ {![]() }.
}.
Các nghiệm của phương trình đã cho là nghiệm của hai phương trình sau :
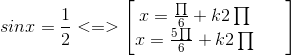
và ![]()
Đáp số : x = ![]() + k2π; x =
+ k2π; x = ![]() + k2π;
+ k2π;
x = arcsin(![]() ) + k2π; x = π - arcsin(
) + k2π; x = π - arcsin(![]() ) + k2π, k ∈ Z.
) + k2π, k ∈ Z.
c) Đặt t = tanx thì phương trình trở thành 2t2 + 3t + 1 = 0 ⇔ t ∈ {-1 ; ![]() }.
}.
Vậy ![]()
d) Đặt t = tanx thì phương trình trở thành
t - ![]() + 1 = 0 ⇔ t2 + t - 2 = 0 ⇔ t ∈ {1 ; -2}.
+ 1 = 0 ⇔ t2 + t - 2 = 0 ⇔ t ∈ {1 ; -2}.
Vậy ![]()

a)ĐKXĐ:\(a\ge0;a\ne16\)
\(B=\left[\dfrac{3\sqrt{a}}{\sqrt{a}+4}+\dfrac{\sqrt{a}}{\sqrt{a}-4}+\dfrac{4\left(a+2\right)}{16-a}\right]:\left(1-\dfrac{2\sqrt{a}+5}{\sqrt{a}+4}\right)\)
=\(\dfrac{3\sqrt{a}\left(\sqrt{a}-4\right)+\sqrt{a}\left(\sqrt{a}+4\right)-4\left(a+2\right)}{a-16}:\dfrac{\sqrt{a}+4-2\sqrt{a}-5}{\sqrt{a}+4}=\dfrac{3a-12\sqrt{a}+a+4\sqrt{a}-4a-8}{\left(\sqrt{a}-4\right)\left(\sqrt{a}+4\right)}\cdot\dfrac{\sqrt{a}+4}{-\sqrt{a}-1}=\dfrac{-8\sqrt{a}-8}{\left(\sqrt{a}-4\right)\left(-\sqrt{a}-1\right)}=\dfrac{8\left(-\sqrt{a}-1\right)}{\left(\sqrt{a}-4\right)\left(-\sqrt{a}-1\right)}=\dfrac{8}{\sqrt{a}-4}\)
Vậy...
b)Với \(a\ge0;a\ne16\) thì B=\(\dfrac{8}{\sqrt{a}-4}\)
B=-3 thì \(\dfrac{8}{\sqrt{a}-4}=-3\)
=>\(9=-3\sqrt{a}+24\)
<=>-15=-3\(\sqrt{a}\)
<=>\(\sqrt{a}=5\)
<=>a=25(TM)
Vậy a=25 thì B=-3
c)Với \(a\ge0;a\ne16\) thì B=\(\dfrac{8}{\sqrt{a}-4}\)
| \(\sqrt{a}-4\) | -8 | -4 | -2 | -1 | 1 | 2 | 4 | 8 |
| \(\sqrt{a}\) | -4(L) | 0 | 2 | 3 | 5 | 6 | 8 | 12 |
| \(\sqrt{a}\) | 0 | 2 | 3 | 5 | 6 | 8 | 12 |
| a | 0(TM) | 4(TM) | 9(TM) | 25(TM) | 36(TM) | 64(TM) | 144(TM) |
(BẠN KẺ 1 BẢNG 3 HÀNG THÔI NHA,MÌNH KẺ LỖI NÊN LÀM 2 BẢNG)
Vậy...

a) Ta có 
Do đó, y'<0 <=>  <=> x≠1 và x2 -2x -3 <0
<=> x≠1 và x2 -2x -3 <0
<=> x≠ 1 và -1<x<3 <=> x∈ (-1;1) ∪ (1;3).
b) Ta có 
Do đó, y’≥0 <=>  <=> x≠ -1 và x2 +2x -3 ≥ 0 <=> x≠ -1 và x ≥ 1 hoặc x ≤ -3 <=> x ≥ 1 hoặc x ≤ -3
<=> x≠ -1 và x2 +2x -3 ≥ 0 <=> x≠ -1 và x ≥ 1 hoặc x ≤ -3 <=> x ≥ 1 hoặc x ≤ -3
<=> x∈ (-∞;-3] ∪ [1;+∞).
c).Ta có 
Do đó, y’>0 <=>
 <=> -2x2 +2x +9>0 <=> 2x2 -2x -9 <0 <=>
<=> -2x2 +2x +9>0 <=> 2x2 -2x -9 <0 <=>  <=> x∈
<=> x∈  vì x2 +x +4 = (x+1/2)2 + 15/4 >0, với ∀ x ∈ R.
vì x2 +x +4 = (x+1/2)2 + 15/4 >0, với ∀ x ∈ R.
TenAnh1 TenAnh1 A = (-0.04, -7.12) A = (-0.04, -7.12) A = (-0.04, -7.12) B = (15.32, -7.12) B = (15.32, -7.12) B = (15.32, -7.12) C = (-4.78, -5.6) C = (-4.78, -5.6) C = (-4.78, -5.6) D = (7.82, -7.32) D = (7.82, -7.32) D = (7.82, -7.32) E = (-4.82, -6.92) E = (-4.82, -6.92) E = (-4.82, -6.92) F = (10.54, -6.92) F = (10.54, -6.92) F = (10.54, -6.92) G = (-7.14, -8.07) G = (-7.14, -8.07) G = (-7.14, -8.07) H = (12.33, -8.07) H = (12.33, -8.07) H = (12.33, -8.07) I = (-1.74, -9.56) I = (-1.74, -9.56) I = (-1.74, -9.56) J = (18.64, -9.56) J = (18.64, -9.56) J = (18.64, -9.56) K = (-7.17, -8.04) K = (-7.17, -8.04) K = (-7.17, -8.04) L = (12.3, -8.04) L = (12.3, -8.04) L = (12.3, -8.04) M = (-7.24, -7.99) M = (-7.24, -7.99) M = (-7.24, -7.99) N = (12.23, -7.99) N = (12.23, -7.99) N = (12.23, -7.99)