Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta có:
- Góc ABD là góc giữa hai phân giác của góc ABC, nên ABD = CBD.
- Góc EBD là góc giữa phân giác của góc ABC và đường thẳng DE, nên EBD = CBD.
Vậy tam giác ABD = tam giác EBD.
b) Ta có:
- Góc ABD = góc EBD (do chứng minh ở câu a).
- Góc ADB = góc EDB (do cùng là góc vuông).
- Vậy tam giác ABD = tam giác EBD (do hai góc bằng nhau và góc giữa hai cạnh bằng nhau).
- Do đó, BD vuông góc với AE.
- Ta có AE cắt BD tại I, vậy I là trung điểm của AE.
c) Ta có:
- Tia Cx vuông góc với tia BD tại H.
- Trên tia đối của tia AB, lấy điểm F sao cho AF = EC.
- Ta cần chứng minh 3 điểm C, H, F thẳng hàng và AE // FC.
- Vì AF = EC và tam giác ABD = tam giác EBD (do chứng minh ở câu a), nên tam giác AFB = tam giác EFC (do hai cạnh bằng nhau và góc giữa hai cạnh bằng nhau).
- Vậy 3 điểm C, H, F thẳng hàng và AE // FC.
a: Xét ΔBAD vuông tại A và ΔBED vuông tại E có
BD chung
\(\widehat{ABD}=\widehat{EBD}\)
Do đó: ΔBAD=ΔBED
b: Ta có: ΔBAD=ΔBED
=>BA=BE và DA=DE
Ta có: BA=BE
=>B nằm trên đường trung trực của AE(1)
Ta có: DA=DE
=>D nằm trên đường trung trực của AE(2)
Từ (1) và (2) suy ra BD là đường trung trực của AE
=>BD vuông góc với AE tại trung điểm I của AE
c: Xét ΔBFC có \(\dfrac{BA}{AF}=\dfrac{BE}{EC}\)
nên AE//CF
Ta có: BD\(\perp\)AE
AE//CF
Do đó: BD\(\perp\)CF
mà BD\(\perp\)CH
và CH,CF có điểm chung là C
nên C,H,F thẳng hàng

e) vì AC vuông góc vs BK , KE ( kéo dài ED)vuông góc với BC mà AC và KE cắt nhau tại D => D là trực tâm của tam giác KBC => BD vuoogn góc với KC ( 1 ) .M là trung điểm của KC => BM là đường cao đồng thời là đường trung trực của tam giác KBC ( 2 ) . từ ( 1 ) và ( 2 ) => B, D , M thằng hàng

ABCDIE12
1) Xét hai tam giác ABI và EBI có:
AB = EB (gt)
B1ˆ=B2ˆ(gt)B1^=B2^(gt)
BI: cạnh chung
Vậy: ΔABI=ΔEBI(c−g−c)ΔABI=ΔEBI(c−g−c)
Suy ra: BAIˆ=BEIˆBAI^=BEI^ (hai góc tương ứng)
Mà BAIˆ=90oBAI^=90o
Do đó: BEIˆ=90oBEI^=90o
2) Xét hai tam giác vuông AID và EIC có:
IA = IE (ΔABI=ΔEBIΔABI=ΔEBI)
AIDˆ=EICˆAID^=EIC^ (đối đỉnh)
Vậy: ΔAID=ΔEIC(cgv−gn)ΔAID=ΔEIC(cgv−gn)
Suy ra: ID = IC (hai cạnh tương ứng)
Do đó: ΔIDCΔIDC cân tại I
3) Ta có: AB = EB (gt)
⇒ΔABE⇒ΔABE cân tại B
⇒⇒ BI là đường phân giác đồng thời là đường trung trực AE
hay BI ⊥⊥ AE (1)
Ta lại có: AB = EB (gt)
AD = EC (ΔAID=ΔEICΔAID=ΔEIC)
=> BD = BC
=> ΔBDCΔBDC cân tại B
=> BI là đường phân giác đồng thời là đường cao của tam giác
hay BI ⊥⊥ DC (2)
Từ (1) và (2) suy ra: AE // DC (đpcm)

a: Xet ΔBAD vuông tại A và ΔBED vuông tại E có
BD chung
góc ABD=góc EBD
=>ΔBAD=ΔBED
b: ΔBAE cân tại B
mà BM là phân giác
nên BM vuông góc AE tại M và M là trung điểm của AE
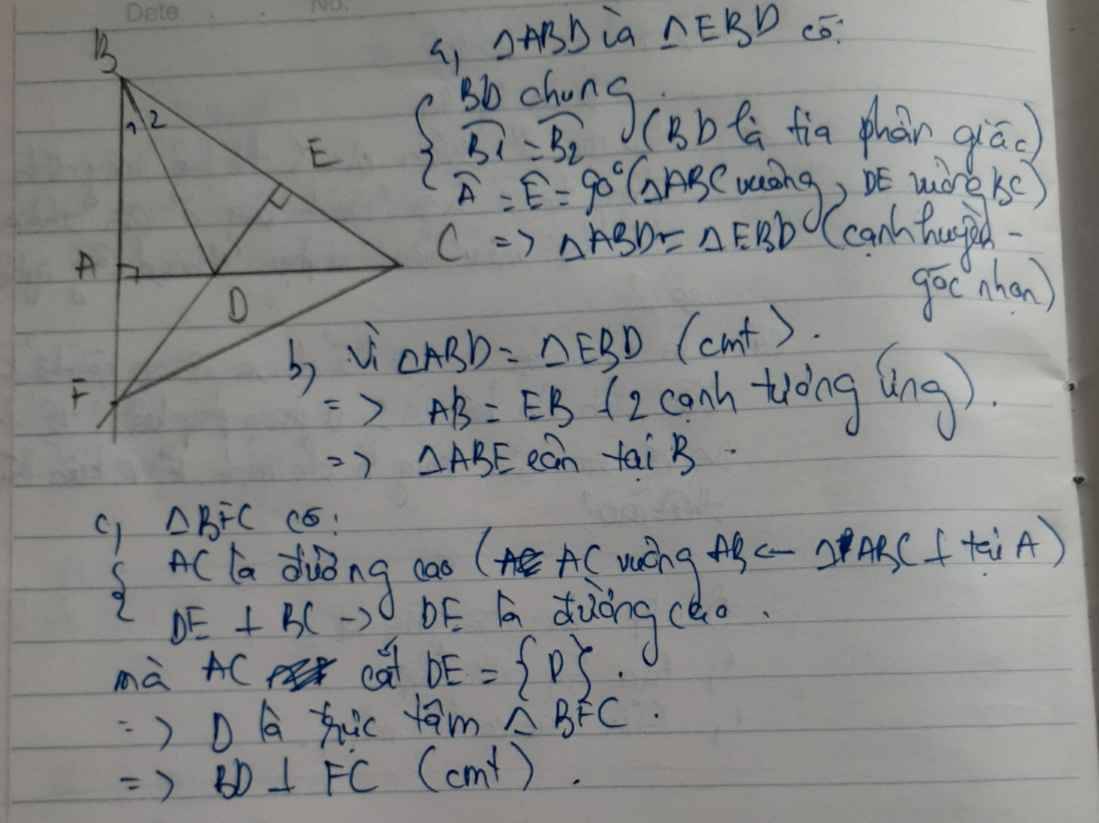
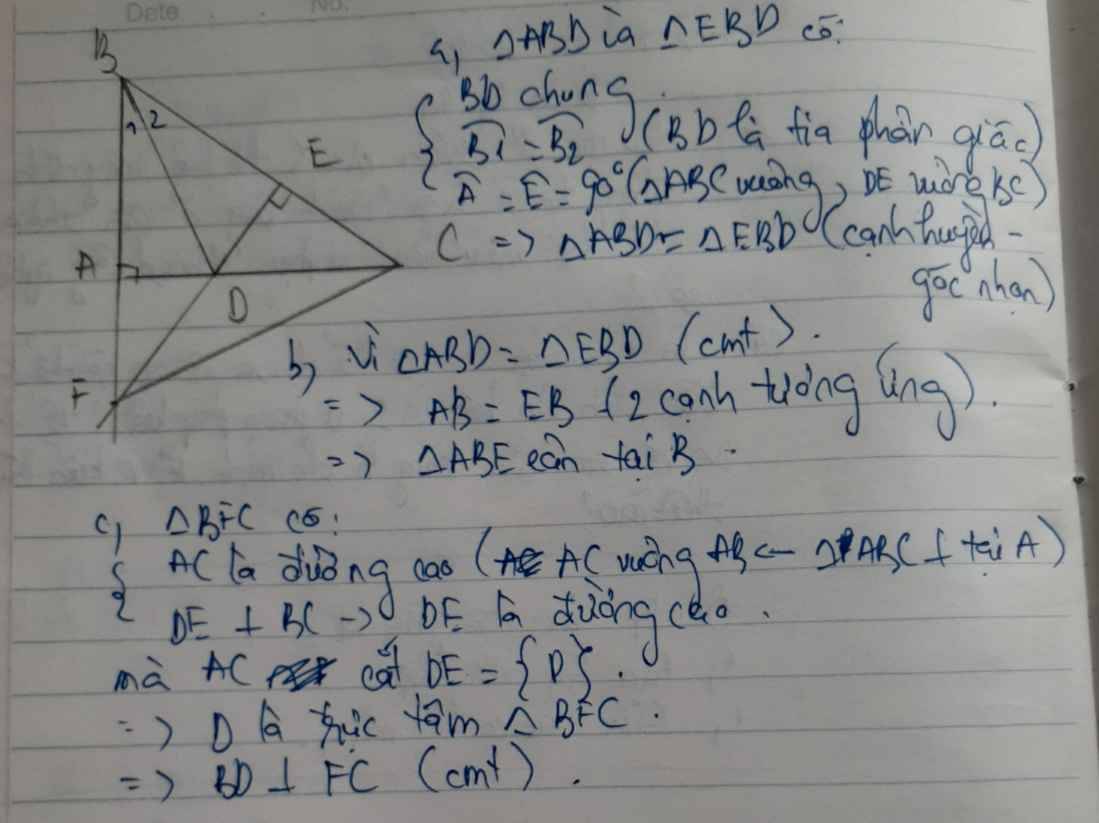

a: Xét ΔBAD vuông tại A và ΔBED vuông tại E có
BD chung
\(\widehat{ABD}=\widehat{EBD}\)
Do đó:ΔBAD=ΔBED
b: ta có: ΔBAD=ΔBED
nên BA=BE
hay ΔBAE cân tại B
c: Ta có: BA=BE
DA=DE
Do đó: BD là đường trung trực của AE
hay BD⊥AE