


Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.





Cho 3 số thực dương a;b;c thỏa mãn : a+ b + c = 1 . CMR
\(\frac{a+1}{a+b+c}+\frac{b+1}{b+ac}+\frac{c+1}{c+ab}\ge9\)Dấu " = " xay ra khi nào

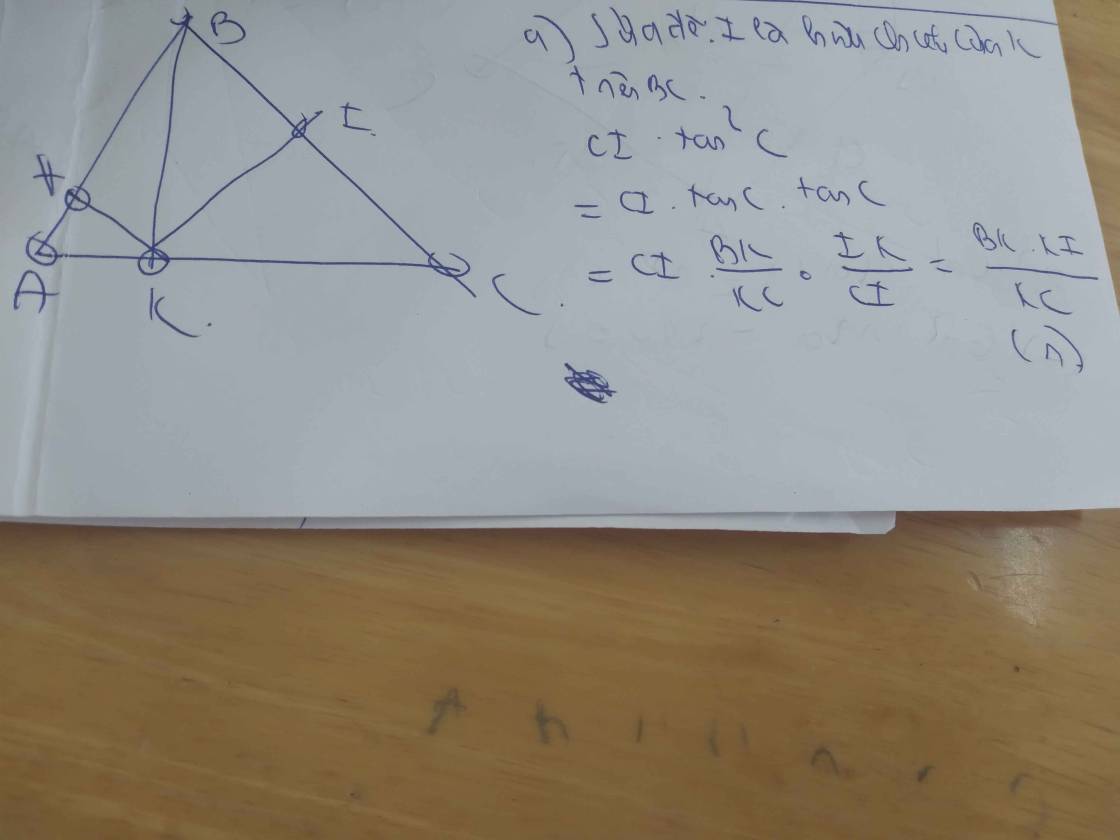
a/ Ta có CF vuông góc AB tại F (gt)
Nên góc CFB = 90 độ
BE vuông góc AC tại E
Nên góc BEC = 90 độ
Tứ giác CEFB có hai đỉnh kề F và E cùng nhìn cạnh BC dưới một góc vuông . Do đó tứ giác CEFB nt
Ta có góc BFC = 90(cmt) độ nên tam giác BFC vuông tại F .
góc BEC = 90 độ (cmt)
Nên tam giác BEC vuông tại E
Tam giác vuông BFC và BEC đều có BC là cạnh huyền nên tâm của đường tròn ngoại tiếp tứ giác là trung điểm của cạnh BC .

\(x^2+6x+5=0\)
<=>\(x^2+x+5x+5=0\)
<=>\(x\left(x+1\right)+5\left(x+1\right)=0\)
<=>\(\left(x+1\right)\left(x+5\right)=0\hept{\begin{cases}x+1=0< =>x=-1\\x+5=0< =>x=-5\end{cases}}\)bấm máy thử nghiệm đc mà .Bài này lớp 8 mà đâu phải lớp 9
x^2+6x+5=0
<=> x^2+x+5x+5=0
<=>x(x+1)+5(x+1)=0
<=> (x+5)(x+1)=0
=> x+5=0 hoặc x+1=0 <=> x=-5 hoặc x=-1

\(A=0.5\cdot4\sqrt{3-x}-\sqrt{3-x}-2\sqrt{3}+1=\sqrt{3-x}-2\sqrt{3}+1\) (xác định khi x=<3)
a)thay \(x=2\sqrt{2}\)vào a ra có
\(\sqrt{3-2\sqrt{2}}-2\sqrt{3}+1=\sqrt{\left(\sqrt{2}-1\right)^2}-2\sqrt{3}+1\)
\(=\sqrt{2}-1+2\sqrt{3}+1=\sqrt{2}+2\sqrt{3}\)
Để A=1<=> \(\sqrt{3-x}-2\sqrt{3}+1=1\\ \Leftrightarrow\sqrt{3-x}-2\sqrt{3}+1-1=0\\ \Leftrightarrow\sqrt{3-x}-2\sqrt{3}=0\\ \Leftrightarrow3-x=12\Leftrightarrow x=-9\)

a)
Xét hiệu \(\frac{a^3}{a^2+1}-\frac{1}{2}=\frac{2a^3-a^2-1}{2\left(a^2+1\right)}=\frac{2a^2\left(a-1\right)+\left(a-1\right)\left(a+1\right)}{2\left(a^2+1\right)}=\frac{\left(a-1\right)\left(2a^2+a+1\right)}{2\left(a^2+1\right)}\)
Do : \(a\ge1\Rightarrow a-1\ge0\)
\(a^2+a+1=\left(a+\frac{1}{4}\right)^2+\frac{3}{4}>0\Rightarrow2a^2+a+1>0\)
\(a^2+1>0\)
\(\Rightarrow\frac{\left(a-1\right)\left(2a^2+a+1\right)}{2\left(a^2+1\right)}\ge0\Leftrightarrow\frac{a^3}{a^2+1}-\frac{1}{2}\ge0\Leftrightarrow\frac{a^3}{a^2+1}\ge\frac{1}{2}\)
Tương tự \(\frac{b^3}{b^2+1}\ge\frac{1}{2};\frac{c^3}{c^2+1}\ge\frac{1}{2}\)
\(\Rightarrow\frac{a^3}{a^2+1}+\frac{b^3}{b^2+1}+\frac{c^3}{c^2+1}\ge\frac{3}{2}\)Dấu = xảy ra khi a=b=c=1