K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

16 tháng 4 2018
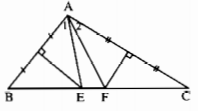
Vì E thuộc đường trung trực của đoạn thẳng AB nên EA = EB, hay tam giác EAB cân tại đỉnh E. Suy ra \(\widehat{B}=\widehat{A_1}\). Tương tự, có \(\widehat{C}=\widehat{A_2}\). Ta có:
\(\widehat{EAF}=\widehat{A}-\left(\widehat{A_1}+\widehat{A_2}\right)=\widehat{A}-\left(\widehat{B}+\widehat{C}\right)\)
Mặt khác
\(\widehat{B}+\widehat{C}=180^0-\widehat{A}=180^0-100^0=80^0\)
a) Góc EAF là góc giữa hai đường trung trực của AB và AC. Do đó, góc EAF sẽ bằng 180o - góc A = 180o - 100o = 80o.
b) Để chứng minh AO là tia phân giác của góc EAF, ta cần chứng minh rằng góc EAO = góc FAO.
Ta biết rằng góc EAO = góc BAO = \(\dfrac{1}{2}\) góc BAC = \(\dfrac{1}{2}\cdot\) 100o = 50o (vì AO là đường trung trực của AB).
Tương tự, góc FAO = góc CAO = \(\dfrac{1}{2}\) góc CAB = \(\dfrac{1}{2}\cdot\) 100o = 50o (vì AO là đường trung trực của AC).
Vì góc EAO = góc FAO, nên AO là tia phân giác của góc EAF.
hơi sai sai