Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Vì \(\Delta ABC \backsim \Delta A'B'C'\) theo tỉ số đồng dạng \(k\) nên \(\frac{{AB}}{{A'B'}} = \frac{{BC}}{{B'C'}} = k;\,\,\widehat B = \widehat {B'}\)
Mà AM và A’M’ lần lượt là trung tuyến của hai tam giác ABC và A’B’C’ nên M và M’ lần lượt là trung điểm của BC và B’C’.
\(\begin{array}{l} \Rightarrow BM = \frac{1}{2}BC;\,\,B'M' = \frac{1}{2}B'C'\\ \Rightarrow \frac{{AB}}{{A'B'}} = \frac{{BM}}{{B'M'}} = k\end{array}\)
Xét tam giác ABM và tam giác A’B’M’ có:
\(\frac{{AB}}{{A'B'}} = \frac{{BM}}{{B'M'}}\) và \(\widehat B = \widehat {B'}\)
\( \Rightarrow \Delta ABM \backsim \Delta A'B'M'\) (c-g-c)
\( \Rightarrow \frac{{AM}}{{A'M'}} = \frac{{BM}}{{B'M'}} = k\)
b) Vì \(\Delta ABC \backsim \Delta A'B'C'\) theo tỉ số đồng dạng \(k\) nên \(\frac{{AB}}{{A'B'}} = \frac{{AC}}{{A'C'}} = k;\,\,\widehat B = \widehat {B'}\)
\(\frac{{AB}}{{AC}} = \frac{{A'B'}}{{A'C'}}\)
Vì AD và A’D’ lần lượt là phân giác của tam giác ABC và tam giác A’B’C’ nên ta có \(\frac{{DB}}{{DC}} = \frac{{AB}}{{AC}}\) và \(\frac{{D'B'}}{{D'C'}} = \frac{{A'B'}}{{A'C'}}\)
\( \Rightarrow \frac{{DB}}{{DC}} = \frac{{D'B'}}{{D'C'}} \Rightarrow \frac{{DB}}{{D'B'}} = \frac{{DC}}{{D'C'}} = \frac{{DB + DC}}{{D'B' + D'C'}} = \frac{{BC}}{{B'C'}}\)
Mà \(\frac{{AB}}{{A'B'}} = \frac{{BC}}{{B'C'}}\) (chứng minh ở câu a) nên \(\frac{{DB}}{{D'B'}} = \frac{{AB}}{{A'B'}}\)
Xét tam giác ABD và tam giác A’B’D’ có:
\(\frac{{BD}}{{B'D'}} = \frac{{AB}}{{A'B'}}\) và \(\widehat B = \widehat {B'}\)
\( \Rightarrow \Delta ABD \backsim \Delta A'B'D'\) (c-g-c)
\( \Rightarrow \frac{{AD}}{{A'D'}} = \frac{{AB}}{{A'B'}} = k\)
c) Ta có \(\widehat B = \widehat {B'}\) và \(\widehat {AHB} = \widehat {A'H'B'} = 90^\circ \)
\( \Rightarrow \Delta ABH \backsim \Delta A'B'H'\) (g-g)
\( \Rightarrow \frac{{AB}}{{A'B'}} = \frac{{AH}}{{A'H'}} = k\)

a) Vì ΔA′B′C′ ∽ ΔABC
=> \(\widehat B = \widehat {B'};\frac{{A'H'}}{{AB}} = \frac{{A'C'}}{{AC}} = \frac{{B'C'}}{{BC}} = k\)
Xét hai tam giác vuông A'H'B' (vuông tại H') và tam giác vuông AHB (vuông tại H), có:
\(\widehat B = \widehat {B'}\)
=> ΔA′H′B′ ∽ ΔAHB
=> \(\frac{{A'H'}}{{AH}} = \frac{{A'B'}}{{AB}}\)
Mà \(\frac{{A'B'}}{{AB}} = k\)
=> \(\frac{{A'H'}}{{AH}} = k\)
b) Có diện tích tam giác ABC là: \(\frac{1}{2}\)AH.BC
Có diện tích tam giác A'B'C' là: \(\frac{1}{2}\)A′H′.B′C′
Xét tỉ lệ giữa hai tam giác A'B'C' và tam giác ABC có:
\(\frac{{\frac{1}{2}A'H'.B'C'}}{{\frac{1}{2}AH.BC}} = \frac{{A'H'}}{{AH}}.\frac{{B'C'}}{{BC}} = k.k = {k^2}\)

a) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=6^2+8^2=100\)
hay BC=10(cm)
Vậy: BC=10cm
a) Xét ΔABC có
BD là đường phân giác ứng với cạnh AC(gt)
nên \(\dfrac{AD}{AB}=\dfrac{CD}{BC}\)(Tính chất tia phân giác của tam giác)
hay \(\dfrac{AD}{6}=\dfrac{CD}{10}\)
mà AD+CD=AC=8(cm)(D nằm giữa A và C)
nên Áp dụng tính chất của dãy tỉ số bằng nhau,ta được:
\(\dfrac{AD}{6}=\dfrac{CD}{10}=\dfrac{AD+CD}{6+10}=\dfrac{8}{16}=\dfrac{1}{2}\)
Do đó:
\(\left\{{}\begin{matrix}\dfrac{AD}{6}=\dfrac{1}{2}\\\dfrac{CD}{10}=\dfrac{1}{2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AD=3\left(cm\right)\\CD=5\left(cm\right)\end{matrix}\right.\)
Vậy: AD=3cm; CD=5cm

a: Xét ΔA'B'C' và ΔABC có
A'B'/AB=A'C'/AC=B'C'/BC
Do đó: ΔA'B'C'\(\sim\)ΔABC
b: \(\dfrac{C_{A'B'C'}}{C_{ABC}}=\dfrac{A'B'}{AB}=2\)

a: \(\widehat{C}=180^0-40^0-80^0=60^0\)
b: \(\dfrac{S_{ABC}}{S_{A'B'C'}}=\left(\dfrac{1}{2}\right)^2=\dfrac{1}{4}\)

a: Xét ΔABH có BI là phân giác
nên \(\dfrac{AI}{AB}=\dfrac{IH}{BH}\)
Xét ΔABC có BD là phân giác
nên \(\dfrac{AD}{AB}=\dfrac{CD}{CB}\)
Đề bài này chưa đủ dữ kiện để tính cụ thể AI/AB; AD/AB nha bạn
b: ΔBAD vuông tại A
=>\(\widehat{ABD}+\widehat{ADB}=90^0\)
=>\(\widehat{ADI}+\dfrac{1}{2}\cdot\widehat{ABC}=90^0\left(1\right)\)
ΔBIH vuông tại H
=>\(\widehat{HBI}+\widehat{BIH}=90^0\)
=>\(\widehat{BIH}+\dfrac{1}{2}\cdot\widehat{ABC}=90^0\)(2)
Từ (1) và (2) suy ra \(\widehat{ADI}=\widehat{BIH}\)
mà \(\widehat{AID}=\widehat{BIH}\)(hai góc đối đỉnh)
nên \(\widehat{ADI}=\widehat{AID}\)
=>ΔAID cân tại A
=>AD=AI(3)
Xét ΔABH có BI là phân giác
nên \(\dfrac{IH}{BH}=\dfrac{AI}{AB}\left(4\right)\)
Xét ΔABC có BD là phân giác
nên \(\dfrac{DC}{BC}=\dfrac{DA}{AB}\left(5\right)\)
Từ (3),(4),(5) suy ra \(\dfrac{IH}{BH}=\dfrac{DC}{BC}\)
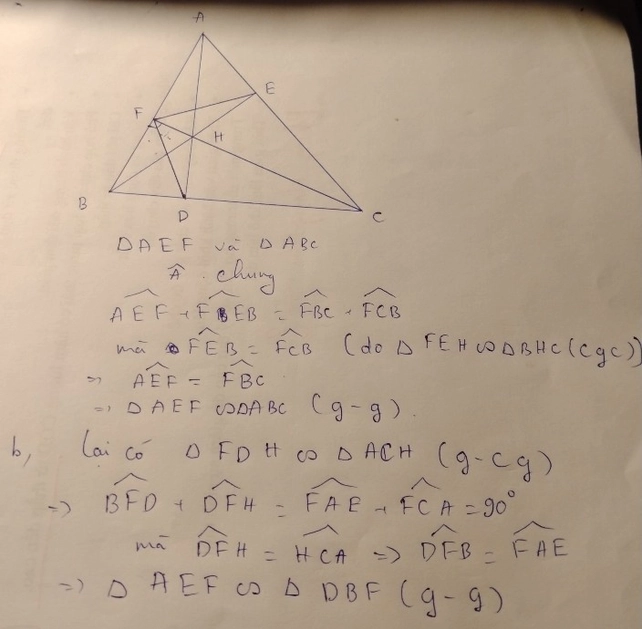
a: AD/A'D'=k=3/2
b: AH/A'H'=3/2
c: AM/A'M'=3/2