K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
PT
1
CM
16 tháng 1 2019
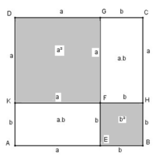
Dựng hình vuông ABCD có cạnh bằng a
Trên cạnh AB lấy điểm E sao cho BE = b
Từ E dựng đường thẳng song song BC cắt CD tại G
Ta có: CG = b, CE = ( a – b ), GD = ( a – b )
Trên cạnh AD lấy điểm K sao cho AK = b
Từ K kẻ đường thẳng song song với AB cắt BC tại H và cắt EG tại F
Ta có: KD = ( a – b ), BH = b
Hình vuông ABCD có diện tích bằng a 2
Hình vuông DKFG có diện tích bằng a - b 2
Hình chữ nhật AEFK có diện tích bằng ( a – b ) b
Hình vuông EBHF có diện tích bằng b 2
Hình chữ nhật HCGF có diện tích bằng ( a – b ).b
S A B C D = S D K F G + S A E F K = S E B H F + S H C G F
nên a - b 2 + a - b b + a - b b + b 2 = a 2
⇒ a - b 2 = a 2 - 2 a b + b 2
PT
1
CM
30 tháng 7 2018
Ta có: a - b 2 ≥ 0 ⇒ a 2 + b 2 - 2 a b ≥ 0
⇒ a 2 + b 2 - 2 a b + 2 a b ≥ 2 a b ⇒ a 2 + b 2 ≥ 2 a b
⇒ a 2 + b 2 . 1 / 2 ≥ 2 a b . 1 / 2 ⇒ a 2 + b 2 / 2 ≥ a b
PT
1
CM
6 tháng 6 2018
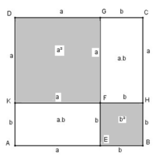
Dựng hình vuông ABCD có cạnh bằng (a + b )
Trên cạnh AB dựng điểm E sao cho AE = a, EB = b, trên cạnh BC dựng điểm H sao cho BH = b, HC = a, trên cạnh CD dựng điểm G sao cho CG = b, GD = a, trên cạnh DA dựng điểm K sao cho DK = a, KA = b, GE cắt KH tại F.
Ta có : diện tích hình vuông ABCD bằng a + b 2
Diện tích hình vuông DKFG bằng a 2
Diện tích hình chữ nhật AKFE bằng a.b
Diện tích hình vuông EBHF bằng b 2
Diện tích hình chữ nhật HCGF bằng a.b
S A B C D = S D K F G + S A K E F + S E B H F + S H C G F
Vậy ta có : a + b 2 = a 2 + 2 a b + b 2
PT
1
CM
28 tháng 10 2018
Từ (1) và (2) suy ra: a 2 < b 2
Ta có: a < b ⇒ a 3 < a 2 b (3)
a < b ⇒ a b 2 < b 3 (4)
a < b ⇒ a.a.b < a.b.b ⇒ a 2 b < a b 2 (5)
Từ (3), (4) và (5) ⇒ a 3 < b 3
PT
1
CM
19 tháng 12 2019
Với a > 0, b > 0 ta có:
a < b ⇒ a.a < a.b ⇒ a 2 < ab (1)
a < b ⇒ a.b < b.b ⇒ ab < b 2 (2)
PT
1
CM
10 tháng 6 2018
Ta có: a + b = 1 ⇔ b = 1 – a
Thay vào bất đẳng thức a2 + b2 ≥ 1/2 , ta được:
a2 + (1 – a)2 ≥ 1/2 ⇔ a2 + 1 – 2a + a2 ≥ 1/2
⇔ 2a2 – 2a + 1 ≥ 1/2 ⇔ 4a2 – 4a + 2 ≥ 1
⇔ 4a2 – 4a + 1 ≥ 0 ⇔ (2a – 1)2 ≥ 0 (luôn đúng)
Vậy bất đẳng thức được chứng minh
TC
6 tháng 5 2022
\(a+b=1=>b=1-a\)
\(=>a^2+\left(1-a\right)^2\ge\dfrac{1}{2}\)
\(=>a^2+1-2a+a^2\ge\dfrac{1}{2}\)
\(\Leftrightarrow-2a+2a^2+1\ge\dfrac{1}{2}\)
\(\Leftrightarrow\left(-2a+2a^2+1\right).2\ge1\)
\(\Leftrightarrow-4a+4a^2+2\ge1\)
\(\Leftrightarrow-4a+4a^2+1\ge0\)
\(\Leftrightarrow\left(2a-1\right)^2\ge0\left(đúng\right)\)
\(''=''\left(khi\right)2a-1=0=>a=\dfrac{1}{2}\)
HP
6 tháng 5 2022
Ta có: \(\left(a-b\right)^2\ge0\)
\(\Leftrightarrow a^2-2ab+b^2\ge0\)
\(\Leftrightarrow a^2+b^2\ge2ab\)
\(\Leftrightarrow a^2+b^2+a^2+b^2\ge2ab+a^2+b^2\)
\(\Leftrightarrow2\left(a^2+b^2\right)\ge\left(a+b\right)^2\)
\(\Leftrightarrow2\left(a^2+b^2\right)\ge1\)
\(\Leftrightarrow a^2+b^2\ge\dfrac{1}{2}\left(đpcm\right)\)
PT
1
7 tháng 6 2021
a)Có \(a^2+1\ge2a\) với mọi a; \(b^2+1\ge2b\) với mọi b
Cộng vế với vế \(\Rightarrow a^2+b^2+2\ge2\left(a+b\right)\)
Dấu = xảy ra <=> a=b=1
b) Áp dụng BĐT bunhiacopxki có:
\(\left(x+y\right)^2\le\left(1+1\right)\left(x^2+y^2\right)\Leftrightarrow\left(x+y\right)^2\le2\)
\(\Leftrightarrow-\sqrt{2}\le x+y\le\sqrt{2}\)
\(\Rightarrow\left(x+y\right)_{max}=\sqrt{2}\Leftrightarrow\left\{{}\begin{matrix}x+y=\sqrt{2}\\x=y\end{matrix}\right.\)\(\Leftrightarrow x=y=\dfrac{\sqrt{2}}{2}\)
\(\left(x+y\right)_{min}=-\sqrt{2}\Leftrightarrow\left\{{}\begin{matrix}x+y=-\sqrt{2}\\x=y\end{matrix}\right.\)\(\Leftrightarrow x=y=-\dfrac{\sqrt{2}}{2}\)
c) \(S=\dfrac{1}{ab}+\dfrac{1}{a^2+b^2}=\dfrac{1}{a^2+b^2}+\dfrac{1}{2ab}+\dfrac{1}{2ab}\)
Với x,y>0, ta có: \(\dfrac{1}{x}+\dfrac{1}{y}\ge\dfrac{4}{x+y}\) (1)
Thật vậy (1) \(\Leftrightarrow\dfrac{y+x}{xy}\ge\dfrac{4}{x+y}\Leftrightarrow\left(x+y\right)^2\ge4xy\)\(\Leftrightarrow\left(x-y\right)^2\ge0\) (lđ)
Áp dụng (1) vào S ta được:
\(S\ge\dfrac{4}{a^2+b^2+2ab}+\dfrac{1}{2ab}\)
Lại có: \(ab\le\dfrac{\left(a+b\right)^2}{4}\) \(\Leftrightarrow2ab\le\dfrac{\left(a+b\right)^2}{2}\Leftrightarrow2ab\le\dfrac{1}{2}\)\(\Rightarrow\dfrac{1}{2ab}\ge2\)
\(\Rightarrow S\ge\dfrac{4}{\left(a+b\right)^2}+2=6\)
\(\Rightarrow S_{min}=6\Leftrightarrow a=b=\dfrac{1}{2}\)
PT
1
CM
31 tháng 7 2019
Biến đổi vế trái ta có:
VT = (a + b)( a 2 – ab + b 2 ) + (a – b)( a 2 + ab + b 2 )
= a 3 + b 3 + a 3 – b 3 = 2 a 3 = VP
Vế trái bằng vế phải nên đẳng thức được chứng minh.
với mọi a, b ta có :
( a - b) ² >= 0
<=> a² - 2ab + b² >= 0
<=> a² + b² >=2ab
<=> 2 ( a² + b² ) >= a² +2ab + b²
<=> 2 (a² + b² ) >= ( a + b )² mà a+b=1 nên 2 ( a² + b² ) >=1
<=> a² + b² >= 1/2
Dấu “ = " xảy ra khi và chỉ khi : a=b mà a+b=1 nên a=b=1/2
nhớ k nha