
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Câu 3:
a: Xét (O) có
CM,CA là các tiếp tuyến
Do đó: CM=CA và OC là phân giác của góc MOA
Ta có: OC là phân giác của góc MOA
=>\(\widehat{MOA}=2\cdot\widehat{MOC}\)
Xét (O) có
DM,DB là các tiếp tuyến
Do đó: DM=DB và OD là phân giác của góc MOB
Ta có: OD là phân giác của góc MOB
=>\(\widehat{MOB}=2\cdot\widehat{MOD}\)
Ta có: \(\widehat{MOA}+\widehat{MOB}=180^0\)(hai góc kề bù)
=>\(2\cdot\left(\widehat{MOD}+\widehat{MOC}\right)=180^0\)
=>\(2\cdot\widehat{COD}=180^0\)
=>\(\widehat{COD}=\dfrac{180^0}{2}=90^0\)
b: Xét ΔCOD vuông tại O có OM là đường cao
nên \(MC\cdot MD=OM^2\)
=>\(AC\cdot BD=OM^2=R^2\)
c: Ta có:AC\(\perp\)AB
BD\(\perp\)AB
Do đó: AC//BD
Xét ΔNCA và ΔNBD có
\(\widehat{NCA}=\widehat{NBD}\)(hai góc so le trong, AC//BD)
\(\widehat{CNA}=\widehat{BND}\)(hai góc đối đỉnh)
Do đó: ΔNCA đồng dạng với ΔNBD
=>\(\dfrac{NC}{NB}=\dfrac{AC}{BD}=\dfrac{NA}{ND}\)
=>\(\dfrac{NA}{ND}=\dfrac{MC}{MD}\)
=>\(\dfrac{DM}{MC}=\dfrac{DN}{NA}\)
Xét ΔDAC có \(\dfrac{DM}{MC}=\dfrac{DN}{NA}\)
nên MN//AC

\(\text{Δ}=\left(-2\right)^2-4\cdot4\cdot\left(m-3\right)\)
\(=4-16\left(m-3\right)=4-16m+48=-16m+52\)
Để phương trình có nghiệm thì -16m+52>=0
=>-16m>=-52
hay m<=13/4
\(\left\{{}\begin{matrix}x_1+x_2=\dfrac{2}{4}=\dfrac{1}{2}\\x_1\cdot x_2=\dfrac{m-3}{4}\end{matrix}\right.\)

ĐK: x>0, 5x-3\(\sqrt{x}\)+8≠ 0
+) 5x-3\(\sqrt{x}\)+8 <0 thì A<0
+)5x-3\(\sqrt{x}\)+8>0, ta có:
\(\frac{1}{5x-3\sqrt{x}+8}\) lớn nhất khi và chỉ khi \(5x-3\sqrt{x}+8\)bé nhất
5x-3\(\sqrt{x}\)+8 ≥ 3/10 ∀x
⇒ Min5x-3\(\sqrt{x}\)+8=3/10
⇒ GTLN của A là 1: 3/10=10/3
Sai thì thôi :v

Ta có a × a < aa = 10 a + a
<=> a < 11(đúng)
aa × aa < aaaa = 100 aa + aa
<=> aa < 101 (đúng)
aaa × aaa < aaaaaa = 1000 aaa + aaa
<=> aaa < 1001 (đúng)
....,..............

 giúp e gấp với aaa
giúp e gấp với aaa
 Giúp tớ câu 3 với aaa:<
Giúp tớ câu 3 với aaa:< giúp e với aaa, e cảm ơn
giúp e với aaa, e cảm ơn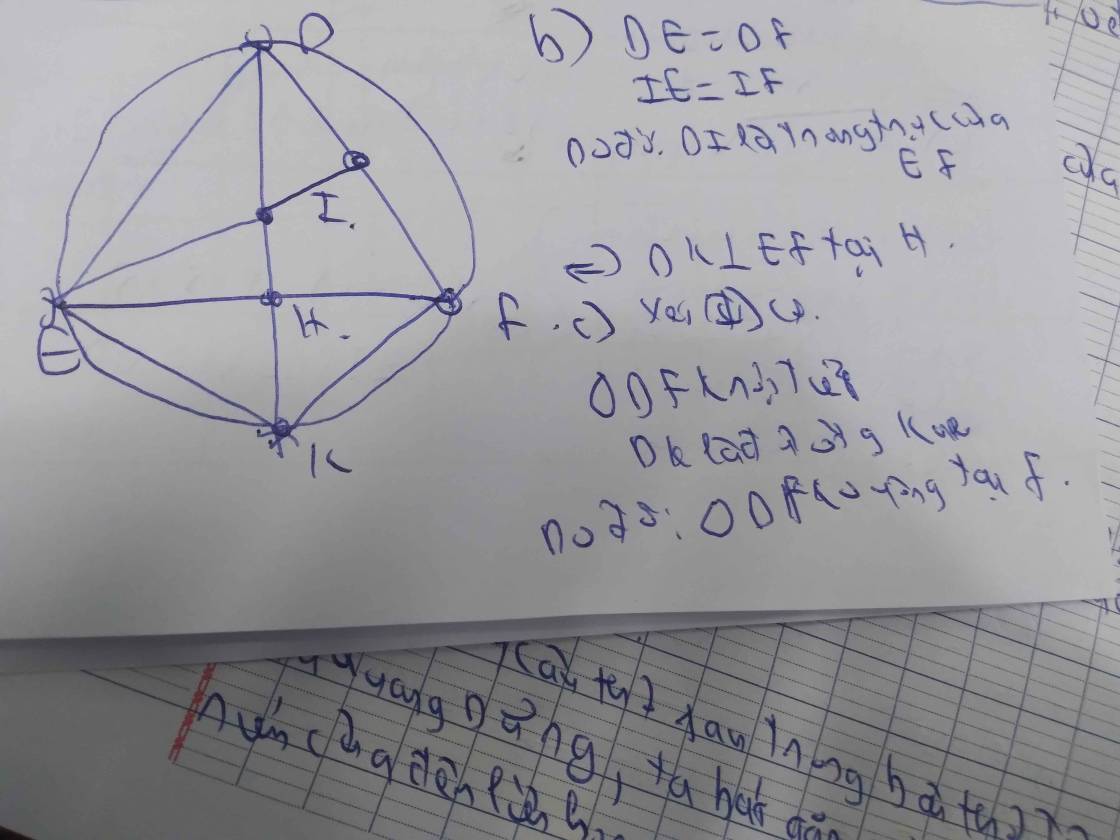

Sai