TT
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
CM
28 tháng 12 2019
a, Số nào chia hết cho 2 mà không chia hết cho 5: 422
b, Số nào chia hết cho 5 mà không chia hết cho 2: 105
c, Số nào chia hết cho cả 2 và 5: 6760
d, Số nào không chia hết cho cả 2 và 5: 3071
CM
27 tháng 9 2017
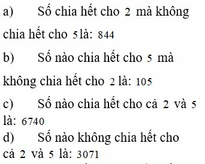
a, Số chia hết cho 2 mà không chia hết cho 5 là: 844
b, Số nào chia hết cho 5 mà không chia hết cho 2 là: 105
c, Số nào chia hết cho cả 2 và 5 là: 6740
d, Số nào không chia hết cho cả 2 và 5 là: 3071
DV
6
H9
HT.Phong (9A5)
CTVHS
9 tháng 8 2023
\(A=5+5^2+...+5^{30}\)
\(A=\left(5+5^2\right)+\left(5^3+5^4\right)+...+\left(5^{29}+5^{30}\right)\)
\(A=\left(5+25\right)+5\cdot\left(5+25\right)+...+5^{28}\cdot\left(5+25\right)\)
\(A=30+5\cdot30+...+5^{28}\cdot30\)
\(A=30\cdot\left(1+5+...+5^{28}\right)\)
Vậy A chia hết cho 30
H9
HT.Phong (9A5)
CTVHS
9 tháng 8 2023
\(A=5+5^2+....+5^{30}\)
\(A=\left(5+5^2+5^3\right)+\left(5^4+5^5+5^6\right)+...+\left(5^{28}+5^{29}+5^{30}\right)\)
\(A=5\cdot\left(1+5+25\right)+5^4\cdot\left(1+5+25\right)+...+5^{28}\cdot\left(1+5+25\right)\)
\(A=5\cdot31+5^4\cdot31+...+5^{28}\cdot31\)
\(A=31\cdot\left(5+5^4+...+5^{28}\right)\)
Vậy A chia hết cho 31
NH
25 tháng 7 2018
Ra A= 5^11-5^3
Vì 5^11chia hết 125
5^3 chia hết cho125
=> 5^11-5^3 chia hết cho125
Lời giải:
$A=(5+5^2)+(5^3+5^4)+...+(5^{29}+5^{30})$
$=(5+5^2)+5^2(5+5^2)+....+5^{28}(5+5^2)$
$=(5+5^2)(1+5^2+....+5^{28})=30(1+5^2+...+5^{28})\vdots 30$
em cảm ơn cô ạ