
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


P=3a-2b\2a+5 + 3b-a\b-5
=2a+a-2b\2a-5 + -a+2b+b\b-5
=2a+(a-2b)\2a-5 + -(a-2b)+b
=2a+5\2a-5 + -5+b\b-5
=-(2a-5)\(2a-5) + (b-5)\(b-5)
=-1+1=0

2,
a, Nếu 2a + 4 \(\ge\) 2b + 4
thì 2a \(\ge\) 2b hay a \(\ge\) b
b, Nếu 3a - 5 \(\le\) 3b - 5
thì 3a \(\le\) 3b hay a \(\le\) b
3,
a, Nếu a \(\le\) b thì a - b \(\le\) 0 hay 2019(a - b) \(\le\) 0 hay 2019a \(\le\) 2019b hay 2019a + 2020 \(\le\) 2019b + 2020
b, Nếu a \(\le\) b thì -a \(\ge\) -b hay -42a \(\ge\) -42b hay -42a - 24 \(\ge\) -42b - 24
3,
a, Nếu a > b thì 3a > 3b hay 3a + 2 > 3b + 2
b, Nếu a > b thì -a < -b hay -4a < -4b hay -4a - 5 < -4b - 5
Chúc bn học tốt!!

a:\(=a^2+10a+25\)
b \(=x^2-2x+1\)
c: \(=9a^2-6a+1\)
d: \(=9b^2-30b+25\)

\(A=\frac{9a^5-ab^4-18a^4b+2b^5}{3a^2b^2+ab^4-6a^2b^3-2b^5}\)
\(=\frac{a\left(9a^4-b^4\right)-2b\left(9a^4-b^4\right)}{ab^2\left(3a^2+b^2\right)-2b^3\left(3a^2+b^2\right)}\)
\(=\frac{\left(9a^4-b^4\right)\left(a-2b\right)}{\left(3a^2+b^2\right)\left(ab^2-2b^3\right)}\)
\(=\frac{\left(3a^2-b^2\right)\left(3a^2+b^2\right)\left(a-2b\right)}{\left(3a^2+b^2\right)b^2\left(a-2b\right)}\)
\(=\frac{3a^2-b^2}{b^2}\)
\(=3.\left(\frac{a}{b}\right)^2-1=3.\left(\frac{2}{3}\right)^2-1=\frac{1}{3}\)

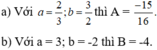
Ta có : a2 + 3a = b2 + 3b
<=> (a2 - b2) + (3a - 3b) = 0
<=> (a - b)(a + b + 3) = 0
<=> \(\left[{}\begin{matrix}a=b\\a=-b-3\end{matrix}\right.\)(1)
Khi đó \(\left\{{}\begin{matrix}a^2+3a=2\\b^2+3b=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left(a+\dfrac{3}{2}\right)^2=\dfrac{17}{4}\\\left(b+\dfrac{3}{2}\right)^2=\dfrac{17}{4}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{\pm\sqrt{17}-3}{2}\\b=\dfrac{\pm\sqrt{17}-3}{2}\end{matrix}\right.\) (2)
Với a = b
Từ (1) và (2) => \(P=a^5+b^5=2a^5=2.\left(\dfrac{\pm\sqrt{17}-3}{2}\right)^5\)
Với a = -b - 3
=> P = \(b^5-\left(b+3\right)^5=\left[{}\begin{matrix}\left(\dfrac{\sqrt{17}-3}{2}\right)^5-\left(\dfrac{\sqrt{17}+3}{2}\right)^5\\\left(\dfrac{-\sqrt{17}-3}{2}\right)^5-\left(\dfrac{-\sqrt{17}+3}{2}\right)^5\end{matrix}\right.\)