NN
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
12 tháng 10 2018
\(\frac{2a+b+c+d}{a}=\frac{a+2b+c+d}{b}=\frac{a+b+2c+d}{c}=\frac{a+b+c+2d}{d}\)
\(\Leftrightarrow\)\(\frac{2a+b+c+d}{a}-1=\frac{a+2b+c+d}{b}-1=\frac{a+b+2c+d}{c}-1=\frac{a+b+c+2d}{d}-1\)
\(\Leftrightarrow\)\(\frac{a+b+c+d}{a}=\frac{a+b+c+d}{b}=\frac{a+b+c+d}{c}=\frac{a+b+c+d}{d}\)
+) Xét \(a+b+c+d=0\)
Suy ra :
\(a+b=-\left(c+d\right)\)
\(b+c=-\left(d+a\right)\)
\(c+a=-\left(b+d\right)\)
\(d+a=-\left(b+c\right)\)
Do đó : \(M=\frac{a+b}{c+d}+\frac{b+c}{d+a}+\frac{c+d}{a+b}+\frac{d+a}{c+b}\)
\(M=\frac{-\left(c+d\right)}{c+d}+\frac{-\left(d+a\right)}{d+a}+\frac{-\left(a+b\right)}{a+b}+\frac{-\left(b+c\right)}{b+c}\)
\(M=\left(-1\right)+\left(-1\right)+\left(-1\right)+\left(-1\right)\)
\(M=-4\)
+) Xét \(a+b+c+d\ne0\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có :
\(\frac{a+b+c+d}{a}=\frac{a+b+c+d}{b}=\frac{a+b+c+d}{c}=\frac{a+b+c+d}{d}=4\)
Do đó :
\(\frac{a+b+c+d}{a}=4\)\(\Leftrightarrow\)\(a+b+c+d=4a\) \(\left(1\right)\)
\(\frac{a+b+c+d}{b}=4\)\(\Leftrightarrow\)\(a+b+c+d=4b\) \(\left(2\right)\)
\(\frac{a+b+c+d}{c}=4\)\(\Leftrightarrow\)\(a+b+c+d=4c\) \(\left(3\right)\)
\(\frac{a+b+c+d}{d}=4\)\(\Leftrightarrow\)\(a+b+c+d=4d\) \(\left(4\right)\)
Từ (1), (2), (3) và (4) suy ra \(4a=4b=4c=4d\) \(\left(=a+b+c+d\right)\)
\(\Leftrightarrow\)\(a=b=c=d\)
\(\Rightarrow\)\(M=\frac{a+a}{a+a}+\frac{b+b}{b+b}+\frac{c+c}{c+c}+\frac{d+d}{d+d}\)
\(\Rightarrow\)\(M=1+1+1+1=4\)
Vậy \(M=-4\) hoặc \(M=4\)
Chúc bạn học tốt ~
12 tháng 10 2018
Ta có :
\(2a+2b+2c=by+cz+ax+cz+ax+by\)
\(\Leftrightarrow\)\(2\left(a+b+c\right)=2\left(ax+by+cz\right)\)
\(\Leftrightarrow\)\(a+b+c=ax+by+cz\)
+) \(a+b+c=ax+\left(by+cz\right)=ax+2a=a\left(x+2\right)\)
\(\Rightarrow\)\(\frac{1}{x+2}=\frac{a}{a+b+c}\) \(\left(1\right)\)
+) \(a+b+c=by+\left(ax+cz\right)=by+2b=b\left(y+2\right)\)
\(\Rightarrow\)\(\frac{1}{y+2}=\frac{b}{a+b+c}\) \(\left(2\right)\)
+) \(a+b+c=cz+\left(ax+by\right)=cz+2c=c\left(z+2\right)\)
\(\Rightarrow\)\(\frac{1}{z+2}=\frac{c}{a+b+c}\) \(\left(3\right)\)
Từ (1), (2) và (3) suy ra \(M=\frac{1}{x+2}+\frac{1}{y+2}+\frac{1}{z+2}\)
\(M=\frac{a}{a+b+c}+\frac{b}{a+b+c}+\frac{c}{a+b+c}\)
\(M=\frac{a+b+c}{a+b+c}=1\)
Vậy \(M=1\)
Chúc bạn học tốt ~
21 tháng 5 2018
Có \(x=by+cz\)
=> \(x\left(1+a\right)=ax+x=ax+by+cz\)
=> \(\frac{1}{1+a}=\frac{x}{ax+by+cz}\)
=> \(\frac{a}{1+a}=\frac{ax}{ax+by+cz}\)
Có \(y=cz+ax\)
=> \(y\left(1+b\right)=by+y=by+cz+ax=ax+by+cz\)
=> \(\frac{1}{1+b}=\frac{y}{ax+by+cz}\)
=> \(\frac{b}{1+b}=\frac{by}{ax+by+cz}\)
Có \(z=ax+by\)
=> \(z\left(1+c\right)=cz+z=cz+ax+by=ax+by+cz\)
=> \(\frac{1}{1+c}=\frac{z}{ax+by+cz}\)
=> \(\frac{c}{1+c}=\frac{cz}{ax+by+cz}\)
=> \(M=\frac{a}{1+a}+\frac{b}{1+b}+\frac{c}{1+c}=\frac{ax}{ax+by+cz}+\frac{by}{ax+by+cz}+\frac{cz}{ax+by+cz}\)
\(=\frac{ax+by+cz}{ax+by+cz}=1\)
Vậy giá trị của M là 1
5 tháng 8 2019
kẻ đường thẳng d // Ax đi qua C,
sử dụng trong cùng phía, so le trong hay đồng vị để tính.
Chúc em làm tốt
NT
1
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
27 tháng 7 2023
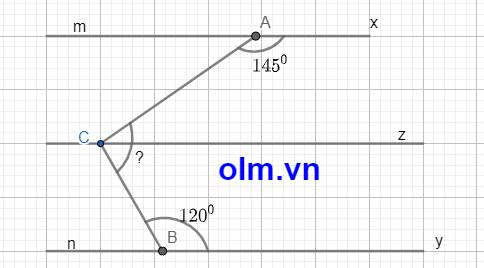
Ta có: \(\widehat{ACz}\) và \(\widehat{CAx}\) là hai góc trong cùng phía nên:
\(\widehat{ACz}\) + \(\widehat{CAx}\) = 1800 ⇒ \(\widehat{ACz}\) = 1800 - 1450 = 350
Mặt khác ta cũng có: \(\widehat{BCz}\) và \(\widehat{CBy}\) là hai góc trong cùng phía nên:
\(\widehat{BCz}\) + \(\widehat{CBy}\) = 1800 ⇒ \(\widehat{BCz}\) = 1800 - 1200 = 600
\(\widehat{ACB}\) = \(\widehat{ACz}\) + \(\widehat{BCz}\) = 350 + 600 = 950
Kết luận: \(\widehat{ACB}\) = 950