Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

*Lời giải chi tiết:
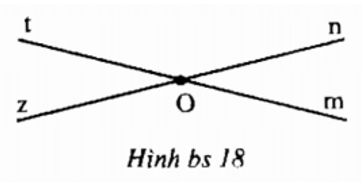
a) Vì góc nOt kề bù với góc mOn nên Ot là tia đối của tia Om. Tương tự, góc mOz kề bù với góc mOn nên Oz là hai tia đối của tia On. Từ đó, zOt và mOn là hai góc đối đỉnh.
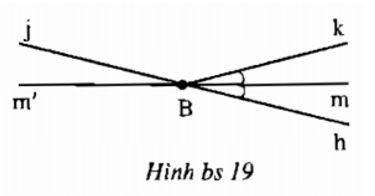
b) Vì góc kBj kề bù với góc hBk nên Bj là tia đối của tia Bh. Từ đó, m’Bj và hBm là hai góc đối đỉnh.
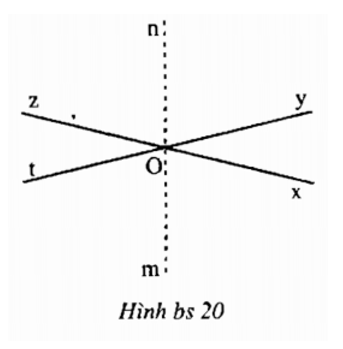
c) Vì góc yOz kề bù với góc xOy nên Oz là tia đối của tia Ox. Tương tự, góc xOt kề bù với góc xOy nên Ot là tia đối của tia Oy. Từ đó, zOy và tOx là hai góc đối đỉnh, tức là ∠zOy = ∠tOx.
Vì On, Om đều là tia phân giác và ∠zOy = ∠tOx nên ∠zOn = ∠nOy = ∠xOm = ∠mOt.
Lại vì ∠zOn + ∠nOx = 180°,
Nên ∠mOx + ∠nOx = 180°.
Suy ra Om và On là hai tia đối nhau.
Từ đó, ∠zOn và ∠mOx là hai góc đối đỉnh.

Mình ko biết đăng hình nên bn tự lên mạng tra nhé :
Đây là 6 cặp góc đối đỉnh !
xOyˆxOy^ đối đỉnh x′Oy′ˆx′Oy′^
xOtˆxOt^ đối đỉnh x′Ot′ˆx′Ot′^
yOtˆyOt^ đối đỉnh y′Ot′ˆy′Ot′^
xOy′ˆxOy′^ đối đỉnh x′Oyˆx′Oy^
x′Otˆx′Ot^ đối đỉnh xOt′ˆxOt′^
yOt′ˆyOt′^ đối đỉnh y′Otˆ
6 cặp góc đối đỉnh :
xOtˆxOt^ đối đỉnh với x′Ot′ˆx′Ot′^ => xOtˆ=x′Ot′ˆxOt^=x′Ot′^ (1)
tOyˆtOy^ đối đỉnh với t′Oy′ˆt′Oy′^ => tOyˆ=t′Oy′ˆtOy^=t′Oy′^ (2)
xOyˆxOy^ đối đỉnh với x′Oy′ˆx′Oy′^ => xOyˆ=x′Oy′ˆxOy^=x′Oy′^ (3)
Ta có: xOyˆ=60xOy^=60 độ =>(3) xOyˆ=x′Oy′ˆ=60xOy^=x′Oy′^=60 độ
Vì Ot là tia phân giác của góc xOy
=> xOtˆ=tOyˆ=602=30xOt^=tOy^=602=30độ
Từ (1),(2) => tOyˆ=t′Oy′ˆ=xOyˆ=x′Oy′ˆ=30tOy^=t′Oy′^=xOy^=x′Oy′^=30độ

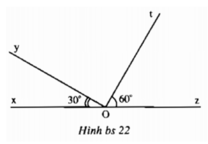
Xem hình bs 22. Rõ ràng hai đường thẳng Ot và Oy cắt nhau tại điểm O. Do góc xOy và góc yOz là hai góc kề bù nên:
∠yOz = 180° - ∠yOx = 150°.
Vì tia Ot nằm giữa hai tia Oz và Oy nên ∠yOt + ∠tOz = ∠yOz, suy ra
∠yOt = ∠yOz - ∠tOz = 150° - 60° = 90°.

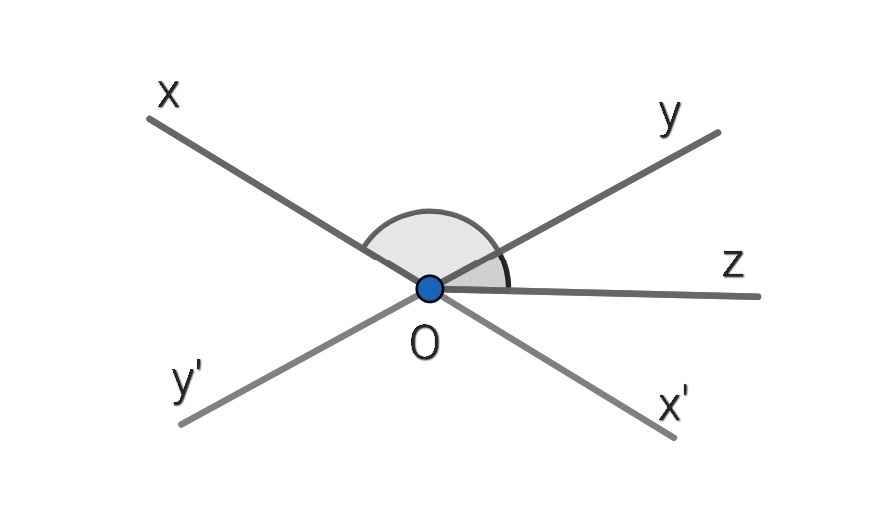 a) Ta có:
a) Ta có:
∠xOy + ∠yOz = 150⁰
∠xOy - ∠yOz = 90⁰
⇒ ∠xOy = (150⁰ + 90⁰) : 2 = 120⁰
⇒ ∠yOz = 120⁰ - 90⁰ = 30⁰
b) Ta có:
∠xOy + ∠x'Oy = 180⁰ (kề bù)
⇒ ∠x'Oy = 180⁰ - ∠xOy
= 180⁰ - 120⁰
= 60⁰