Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Từ Hình 1.20, ta thấy đường thẳng \(y = \frac{1}{2}\) cắt đường tròn tại 2 điểm M, M’. Ta có nghiệm của phương trình là: \(\frac{\pi }{6}, - \frac{{5\pi }}{6}\)
b) Vì hàm số \(\cos x\) tuần hoàn với chu kỳ là \(2\pi \), ta có công thức nghiệm của phương trình là: \(\left[ {\begin{array}{*{20}{c}}{x = \frac{\pi }{6} + k2\pi }\\{x = \pi - \frac{\pi }{6} + k2\pi }\end{array}\;\left( {k \in \mathbb{Z}} \right)} \right.\)

a) Từ Hình 1.25, ta thấy đường thẳng \(y = - 1\) cắt đồ thị hàm số \(y = \cot x\;\)tại 1 điểm \(x = - \frac{\pi }{4} + \pi \) trên khoảng \(\left( {0;\pi } \right)\)
b) Ta có công thức nghiệm của phương trình là: \(x = - \frac{\pi }{4} + \pi + k\pi \;\left( {k \in \mathbb{Z}} \right)\)

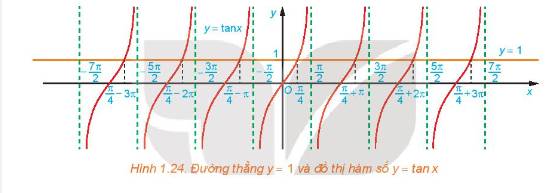
a) Từ Hình 1.24, ta thấy đường thẳng \(y = 1\) cắt đồ thị hàm số \(y = \tan x\;\)tại 1 điểm \(x = \frac{\pi }{4}\) trên khoảng \(\left( { - \frac{\pi }{2};\frac{\pi }{2}} \right)\)
b) Ta có công thức nghiệm của phương trình là: \(x = \frac{\pi }{4} + k\pi \;\left( {k \in \mathbb{Z}} \right)\)

a: Đường thẳng y=1 cắt đồ thị y=tanx tại một điểm duy nhất là \(\left(\dfrac{\Omega}{4};1\right)\)
b: \(tanx=1\)
=>\(x=\dfrac{\Omega}{4}+k\Omega\left(k\in Z\right)\)

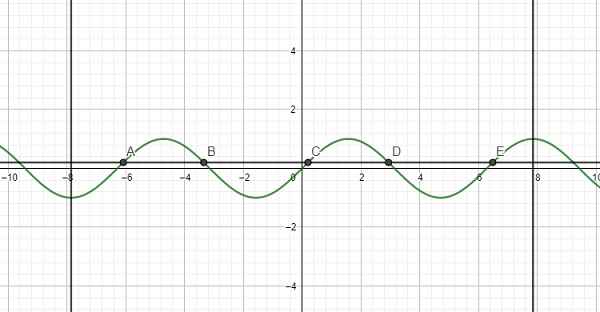
\(0< \dfrac{1}{2018}< 1\)
Kẻ 1 đường thẳng nằm ngang nằm giữa \(y=0\) và \(y=1\) ta thấy cắt đồ thị tại 5 điểm trên đoạn đã cho
\(\Rightarrow\) Pt có 5 nghiệm

Lời giải:
$2\cos ^22x+5\cos 2x-3=0$
$\Leftrightarrow (2\cos 2x-1)(\cos 2x+3)=0$
$\Leftrightarrow 2\cos 2x-1=0$ (chọn) hoặc $\cos 2x=-3$ (loại)
Vậy $2\cos 2x-1=0$
$\Leftrightarrow \cos 2x=\frac{1}{2}$
$\Rightarrow x=\frac{\pm \pi}{3}+2k\pi$ với $k$ nguyên
Để nghiệm trong khoảng $(0;2\pi)$ thì $k=0$ với họ nghiệm $(1)$ và $k=1$ với họ nghiệm $(2)$
Vậy nghiệm của pt thỏa đề là:
$x=\frac{\pi}{3}; x=\frac{5}{3}\pi$
Tổng nghiệm: $\frac{\pi}{3}+\frac{5\pi}{3}=2\pi$

\(\cos5x=-\sin4x\)
<=> \(\cos5x=\cos\left(4x+\frac{\pi}{2}\right)\)
\(\Leftrightarrow\orbr{\begin{cases}5x=4x+\frac{\pi}{2}+k2\pi\\5x=-4x-\frac{\pi}{2}+k2\pi\end{cases}\Leftrightarrow}\orbr{\begin{cases}x=\frac{\pi}{2}+k2\pi\\x=-\frac{\pi}{18}+\frac{k2\pi}{9}\end{cases}}\)
Nghiệm âm lớn nhất: \(-\frac{\pi}{18}\)
Nghiệm dương nhỏ nhất: \(\frac{\pi}{2}\)
pt <=> \(\sin\left(5x+\frac{\pi}{3}\right)=\sin\left(2x-\frac{\pi}{3}+\frac{\pi}{2}\right)\)
<=> \(\sin\left(5x+\frac{\pi}{3}\right)=\sin\left(2x+\frac{\pi}{6}\right)\)
<=> \(\orbr{\begin{cases}5x+\frac{\pi}{3}=2x+\frac{\pi}{6}+k2\pi\\5x+\frac{\pi}{3}=\pi-2x-\frac{\pi}{6}+k2\pi\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}x=-\frac{\pi}{18}+\frac{k2\pi}{3}\\x=\frac{\pi}{14}+\frac{k2\pi}{7}\end{cases}}\)
Trên \(\left[0,\pi\right]\)có các nghiệm:
\(\frac{11\pi}{18},\frac{\pi}{14},\frac{5\pi}{14},\frac{9\pi}{14},\frac{13\pi}{14}\)
tính tổng:...
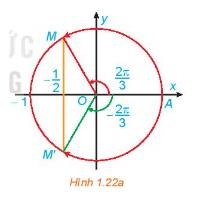

a) Từ Hình 1.19, ta thấy đường thẳng \(y = \frac{1}{2}\) cắt đường tròn tại 2 điểm M, M’. Ta có nghiệm của phương trình là: \(\frac{\pi }{6}, - \frac{{5\pi }}{6}\)
b) Vì hàm số \(\sin x\) tuần hoàn với chu kỳ là \(2\pi \), ta có công thức nghiệm của phương trình là: \(\left[ {\begin{array}{*{20}{c}}{x = \frac{\pi }{6} + k2\pi }\\{x = \pi - \frac{\pi }{6} + k2\pi }\end{array}\;\left( {k \in \mathbb{Z}} \right)} \right.\)