Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) 16(12 t 2 +1).
b) Gợi ý x 3 + y 3 = ( x + y ) 3 - 3xy(x + y)
(x + y - z)( x 2 + y 2 + z 2 - xy + xz + yz).

a)(a+b+c)3 - a3 - b3 - c3
= (a+b+c-a)( a2+b2+c2+2ab+2bc+2ac-a2-ab-ac+a2) - (b+c)(b2-bc+c2)
=(b+c)(a2+ab+ac+bc)
b) x3+y3+z3-3xyz
= (x+y)3-3xy(x+y) +z3-3xyz
= (x+y+z)(x2+y2+2xy-xz-yz+z2) - 3xy(x+y+z)
=(x+y+z)( x2+y2+z2-xy-yz-xz)

a) 12x. b) 4xy
c) 2y(3 x 2 + y 2 ).
d) (x + y + z)( x 2 + y 2 + z 2 – xy – xz - yz).

a) \(x^3+y^3+z^3-3xyz\)
\(=x^3+3x^2y+3xy^2+y^3+z^3-3x^2y-3xy^3-3xyz\)
\(=\left(x+y\right)^3+z^3-3xy\left(x+y+z\right)\)
\(=\left(x+y+z\right)\left[\left(x+y\right)^2-\left(x+y\right)z+z^2\right]-3xy\left(x+y+z\right)\)
\(=\left(x+y+z\right)\left(x^2+2xy+y^2-xz-yz+z^2\right)-3xy\left(x+y+z\right)\)
\(=\left(x+y+z\right)\left(x^2+2xy+y^2-xz-yz+z^2-3xy\right)\)
\(=\left(x+y+z\right)\left(x^2+y^2+z^2-xy-xz-yz\right)\)

\(1.\) \(\left(a+2\right)\left(a+3\right)\left(a^2+a+6\right)+4a^2=\left(a^2+5a+6\right)\left(a^2+a+6\right)+4a^2\)
Đặt \(t=a^2+3a+6\) , ta được:
\(\left(t+2a\right)\left(t-2a\right)+4a^2=t^2-4a^2+4a^2=t^2=\left(a^2+3a+6\right)^2\)

Ta có:
\(a+\frac{1}{b}=b+\frac{1}{c}\)\(\Leftrightarrow\) \(a-b=\frac{1}{c}-\frac{1}{b}\)\(\Leftrightarrow\) \(\left(a-b\right)=\frac{b-c}{bc}\) (1)
\(a+\frac{1}{b}=c+\frac{1}{a}\)\(\Leftrightarrow\)\(a-c=\frac{1}{a}-\frac{1}{b}\)\(\Leftrightarrow\) \(\left(a-c\right)=\frac{b-a}{ab}\) (2)
\(c+\frac{1}{a}=b+\frac{1}{c}\)\(\Leftrightarrow\) \(c-b=\frac{1}{c}-\frac{1}{a}\)\(\Leftrightarrow\) \(\left(c-b\right)=\frac{a-c}{ac}\) (3)
Nhân từng vế của (1)(2)(3) ta được \(\left(a-b\right)\left(a-c\right)\left(c-b\right)=\frac{\left(b-c\right)\left(b-a\right)\left(a-c\right)}{\left(abc\right)^2}=\frac{\left(c-b\right)\left(a-b\right)\left(a-c\right)}{\left(abc\right)^2}\)
\(\Rightarrow abc=\pm1\).

a, x^4 - 5x^2 + 4
= x^4 - 4x^2- x+ 4
= x^2 . (x^2 - 4) - (x^2 - 4)
= (x^2 - 4) . (x^2 - 1)
= (x - 2) . (x + 2) . (x - 1) . (x + 1)
\(\left(x+y+z\right)^3-x^3-y^3-z^3\)
\(=\left(x+y\right)^3+3\left(x+y\right)z\left(x+y+z\right)+z^3-x^3-y^3-z^3\)
\(=x^3+y^3+z^3+3xy\left(x+y\right)+3\left(x+y\right)z\left(x+y+z\right)\)
\(=3\left(x+y\right)\left(xy+xz+yz+z^2\right)\)
\(=3\left(x+y\right)\left(y+z\right)\left(z+x\right)\)

\(\left(a+b\right)^3-\left(a-b\right)^3\)
\(=a^3+3a^2b+3ab^2+b^3-\left(a^3-3a^2b+3ab^2-b^3\right)\)
\(=a^3+3a^2b+3ab^2+b^3-a^3+3a^2b-3ab^2+b^3\)
\(=6a^2b+2b^3\)
\(=2b\left(3a^2+b^2\right)\)
a/\(\left(a+b\right)^3-\left(a-b\right)^3\)
\(=\left(a^3+3a^2b+3ab^2+b^3\right)-\left(a^3-3a^2b+3ab^2-b^3\right)\)\(=a^3+3a^2b+3ab^2+b^3-a^3+3a^2b-3ab^2+b^2\)
\(=6ab^2+2b^3\)(rút gọn hết)
b/\(x^3+y^3+z^3-3xyz\)
\(=\left(x+y\right)^3-3xy\left(x-y\right)+z^3-3xyz\)
\(=\left[\left(x+y\right)^3+z^3\right]-3xy\left(x+y+z\right)\)
\(=\left(x+y+z\right)^3-3z\left(x+y\right)\left(x+y+z\right)-3xy\left(x-y-z\right)\)
\(=\left(x+y+z\right)\left[\left(x+y+z\right)^2-3z\left(x+y\right)-3xy\right]\)
\(=\left(x+y+z\right)\left(x^2+y^2+z^2+2xy-2xz+2xz+2xy-3xz-3yz-3xy\right).\)
\(=\left(x+y+z\right)\left(x^2+y^2+z^2-xy-xz-yz\right)\)
Hok tốt
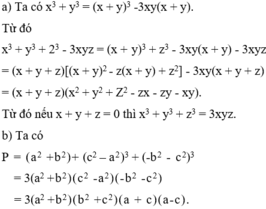
a: =(x+y)^3+z^3-3xy(x+y)-3xyz
=(x+y+z)(x^2+2xy+y^2-xz-yz+z^2)-3xy(x+y+z)
=(x+y+z)(x^2+y^2+z^2-xy-xz-yz)
b: a+b+c<>0
A=(a+b+c)^3-a^3-b^3-c^3/a+b+c
=(a+b+c)(a^2+b^2+c^2-ab-ac-bc)/(a+b+c)
=a^2+b^2+c^2-ab-ac-bc
=1/2[a^2-2ab+b^2+b^2-2bc+c^2+a^2-2ac+c^2]
=1/2[(a-b)^2+(b-c)^2+(a-c)^2]>=0