Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Đa thức biểu thị diện tích mảnh vườn là: \(xy\left(m^2\right)\)
b) Chiều rộng mảnh vườn mới là: \(x+2\left(m\right)\)
Chiều dài mảnh vườn mới là: \(y+3\left(m\right)\)
Đa thức biểu thị diện tích mảnh vườn mới là:
\(\left(x+2\right)\left(y+3\right)=xy+3x+3y+6\left(m^2\right)\)
c) Đa thưc biểu thị phần diện tích lớn hơn của mảnh vườn mới so với mảnh vườn ban đầu là:
\(xy+3x+3y+6-xy=3x+3y+6\left(m^2\right)\)
a, Diện tích mảnh vườn: x.y (m2)
b, Diện tích mảnh vườn mới: \(\left(x+2\right).\left(y+3\right)\left(m^2\right)\)
c, Diện tích phần lớn hơn:
\(\left(x+2\right)\left(y+3\right)-xy=\left(xy+2y+3x+6\right)-xy=2y+3y+6\left(m^2\right)\)

a) Đa thức biểu thị chu vi hình chữ nhật là:
\(\left(2x+y+2x-y\right)\cdot2=4x\cdot2=8x\left(m\right)\)
b) Đa thức biểu thị diện tích hình chữ nhật là:
\(\left(2x+y\right)\left(2x-y\right)=\left(2x\right)^2-y^2=4x^2-y^2\left(m^2\right)\)
c) Diện tích của mảnh vườn là:
\(4\cdot3^2-2^2=32\left(m^2\right)\)
\(a,Chu.vi:2.\left(2x+y+2x-y\right)=2.4x=8x\left(m\right)\\ b,Diện.tích:\left(2x+y\right)\left(2x-y\right)=\left(2x\right)^2-y^2=4x^2-y^2\left(m^2\right)\\ c,Thay:x=3;y=2.vào.biểu.thức.tính.diện.tích.thì.diện.tích.mảnh.vườn.là:\\ 4x^2-y^2=4.3^2-2^2=32\left(m^2\right)\)

a) Đa thức biểu thị diện tích mảnh vườn:
a.(b - 6) (m²)
b) Diện tích mảnh vườn khi a = 14 m; b = 16 m:
14 . (16 - 6) = 14.10 = 140 (m²)

a) Biểu thức tính diện tích của mảnh vườn là: x.y (m2)
b) Chiều rộng mới là: (x + 2) (m)
Chiều dài mới là: (y - 3) (m)
Diện tích mảnh vườn mới là: (x + 2).(y – 3) (m2)
c) Đa thức biểu thị phần diện tích lớn hơn của mảnh vườn so với mảnh vườn ban đầu là:
(x + 2).(y – 3) – xy = xy – 3x + 2y – 6 – xy = 2y – 3x – 6 (m2)

Bài 10:
a: ABCD là hình bình hành
=>\(\widehat{BAD}=\widehat{BCD}\)
mà \(\widehat{BAD}=110^0\)
nên \(\widehat{BCD}=110^0\)
ABCD là hình bình hành
=>\(\widehat{BAD}+\widehat{ABC}=180^0\)
=>\(\widehat{ABC}+110^0=180^0\)
=>\(\widehat{ABC}=70^0\)
ABCD là hình bình hành
=>\(\widehat{ABC}=\widehat{ADC}\)
mà \(\widehat{ABC}=70^0\)
nên \(\widehat{ADC}=70^0\)
b: ABCD là hình bình hành
=>AB=CD(1)
K là trung điểm của AB
=>\(KA=KB=\dfrac{AB}{2}\left(2\right)\)
I là trung điểm của CD
=>\(IC=ID=\dfrac{DC}{2}\left(3\right)\)
Từ (1),(2),(3) suy ra AK=KB=DI=IC
Xét tứ giác AKCI có
AK//CI
AK=CI
Do đó: AKCI là hình bình hành
=>AI//CK
c:Ta có: ABCD là hình bình hành
=>AC cắt BD tại trung điểm của mỗi đường
mà O là trung điểm của BD
nên O là trung điểm của AC
AKCI là hình bình hành
=>AC cắt KI tại trung điểm của mỗi đường
mà O là trung điểm của AC
nên O là trung điểm của KI
=>K,O,I thẳng hàng
Bài 9:
a: Thời gian theo kế hoạch tổ phải hoàn thành công việc là: \(\dfrac{600}{x}\left(giờ\right)\)
b: Thời gian thực tế tổ đã hoàn thành công việc là: \(\dfrac{600}{x+20}\left(giờ\right)\)
c: Thời gian tổ hoàn thành sớm công việc là: \(\dfrac{600}{x}-\dfrac{600}{x+20}\)
\(=\dfrac{600x+12000-600x}{x\left(x+20\right)}=\dfrac{12000}{x\left(x+20\right)}\)
d: Thời gian thực tế hoàn thành công việc là: \(\dfrac{12000}{80\cdot\left(80+20\right)}=\dfrac{12000}{80\cdot100}=\dfrac{12000}{8000}=1,5\left(giờ\right)\)

a) \(S = {x^2} - {\left( {x - 2y} \right)^2}\)
b) \(S = {x^2} - {\left( {x - 2y} \right)^2} = \left( {x - x + 2y} \right)\left( {x + x - 2y} \right) = 2y.\left( {2x - 2y} \right) = 2y.2\left( {x - y} \right) = 4y\left( {x - y} \right)\)
Khi x=102 m, y=2 m thì \(S = 4.2.\left( {102 - 2} \right) = 800\) (\({m^2}\))

a: s=(2x+5)(x-2)
\(=2x^2-4x+5x-10\)
\(=2x^2+x-10\)
b: Khi x=12 thì \(s=2\cdot12^2+12-10=2\cdot144+2=288+2=290\left(cm^2\right)\)
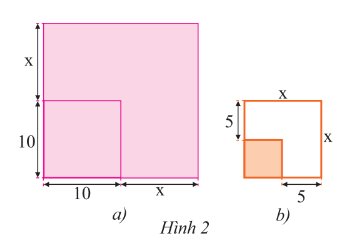
a) Độ dài cạnh mảnh vườn hình vuông sau khi mở rộng là: \(x + 10\) (m)
Diện tích mảnh vườn sau khi mở rộng là:
\(\left( {x + 10} \right)\left( {x + 10} \right) = {\left( {x + 10} \right)^2} = {x^2} + 2.x.10 + {10^2} = {x^2} + 20x + 100\) (\({m^2}\))
b) Độ dài cạnh mảnh vườn hình vuông trước khi mở rộng là: \(x - 5\) (m)
Diện tích mảnh vườn hình vuông trước khi mở rộng là: \(\left( {x - 5} \right)\left( {x - 5} \right) = {\left( {x - 5} \right)^2} = {x^2} - 2.x.5 + {5^2} = {x^2} - 10x + 25\) (\({m^2}\))