Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1/ \(2C^k_n+5C^{k+1}_n+4C^{k+2}_n+C^{k+3}_n\)
\(=2\left(C^k_n+C_n^{k+1}\right)+3\left(C^{k+1}_n+C^{k+2}_n\right)+\left(C^{k+2}_n+C^{k+3}_n\right)\)
\(=2C_{n+1}^{k+1}+3C_{n+1}^{k+2}+C_{n+1}^{k+3}\)
\(=2\left(C_{n+1}^{k+1}+C_{n+1}^{k+2}\right)+\left(C_{n+1}^{k+2}+C^{k+3}_{n+1}\right)\)
\(=2C_{n+2}^{k+2}+C_{n+2}^{k+3}=C_{n+2}^{k+2}+\left(C_{n+2}^{k+2}+C_{n+2}^{k+3}\right)=C_{n+2}^{k+2}+C_{n+3}^{k+3}\)
Áp dụng ct:C(k)(n)=C(k)(n-1)+C(k-1)(n-1) có:
................C(k-1)(n-1)= C(k)(n) - C(k)(n-1)
tương tự: C(k-1)(n-2)= C(k)(n-1) - C(k)(n-2)
................C(k-1)(n-3)= C(k)(n-2) -C(k)(n-3)
.........................................
................C(k-1)(k-1)= C(k)(k) (=1)
Cộng 2 vế vào với nhau...-> đpcm

Điều kiện là n\(\ge\)5, n\(\in\)Z
Ta có
\(\Leftrightarrow\) \(C_{n+1}^5\) = 3\(C_{n+1}^6\) (áp dụng công thức \(C_{n+1}^k\) = \(C_n^k\) + \(C_n^{k-1}\))
\(\Leftrightarrow\) \(\frac{\left(n+1\right)!}{\left(n-4\right)!5!}\) = 3\(\frac{\left(n+1\right)!}{\left(n-5\right)!6!}\)
\(\Leftrightarrow\) \(\frac{1}{\left(n-4\right)!5!}\) = \(\frac{3}{\left(n-5\right)!6!}\)
\(\Leftrightarrow\) \(\frac{1}{n-4}\) = \(\frac{3}{6}\)
\(\Leftrightarrow\) 3n - 12 = 6
\(\Leftrightarrow\) n = 6
Rõ ràng n = 6 thỏa mãn điều kiện n\(\ge\) 5, n \(\in\) Z. Vậy nghiệm duy nhất của chương trình đã cho là n = 6.

Ta có :
\(C^{k+1}_{n+1}=C^k_n+C_n^{k+1}\)
\(C^{k+1}_n=C^k_{n-1}+C_{n-1}^{k+1}\)
...........
\(C^{k+1}_{k+2}=C^k_{k+1}+C_{k+1}^{k+1}\)
Từ đó :
\(C^{k+1}_{n+1}=C^k_n+C_{n-1}^k+....C^k_{k+1}+C^{k+1}_{k+1}\)
= \(C^k_n+C_{n-1}^k+....+C^k_{k+1}+C^k_k\)
Cho số tự nhiên n ≥ 4. Nếu \(C_n^4\) = K thì \(A^4_n\) bằng:
A. 24K
B. 4K
C. 16K
D. \(\frac{K}{24}\)

a) Cách thứ nhất: Chọn 9 bạn nam trong 50 bạn để làm trực nhật. Có 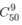 cách.
cách.
Khi đã chọnđược 9 bạn rồi, chọn 4 trong 9 bạn đó để quét sân. Có 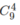 cách.
cách.
Từ đó, theo quy tắc nhân, có 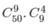 cách phân công.
cách phân công.
Cách thứ hai: Chọn 4 trong 50 bạn để quét sân, sau đó chọn 5 trong 46 bạn còn lại để xén cây. Vậy có 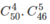 cách phân công.
cách phân công.
Từ đó ta có đẳng thức cần chứng minh.


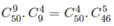
a) Chọn 4 trong 50 bạn để quét sân, sau đó chọn 5 trong 46 bạn còn lại để xén cây. Vậy có \(C^4_{50}.C^4_{46}\) cách phân công.
Từ đó ta có đẳng thức cần chứng minh
b) Lập luận tương tự
c) Ta có : \(0!=1;2!=2;4!=1.2.3.4=24\)
Các số hạng \(6!;8!;.....,100!\) đều có tận cùng là chữ số \(0\). Do đó chữ số ở hàng đơn vị của \(S\) là \(1+2+4=7\)